题目内容
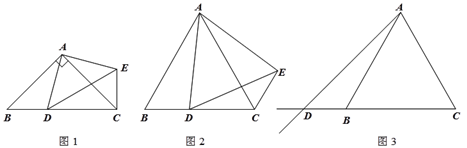
【题目】如图所示，A、D、E三点在同一直线上，
，
，
于点D，
于点E.
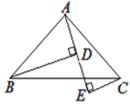
（1）求证：△BAD≌△ACE．
（2）判断BD、DE、CE之间的数量关系，并证明你的结论.
【答案】（1）详见解析；（2）BD= DE+CE，理由详见解析.
【解析】
（1）根据已知条件易证∠BAD=∠ACE，再利用AAS即可证明△ABD≌△ACE；（2）BD= DE+CE，由△ABD≌△ACE，根据全等三角形的性质可得AD=CE，BD=AE，由此即可证得结论.
（1）证明：∵
，
∴AB=AC，
∵
，
，
∴∠ADB=∠CEA=90°，
∴∠EAC+∠ACE=90°，
∵∠BAC=90°，
∴∠BAD+∠EAC=90°，
∴∠BAD=∠ACE，
在△BAD和△ACE，
，
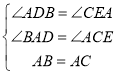∴△BAD≌△ACE（AAS）;
（2）BD= DE+CE，理由如下：
∵△ABD≌△ACE，
∴AD=CE，BD=AE，
∴BD=AE=AD+DE=DE+CE.
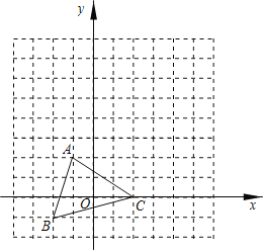
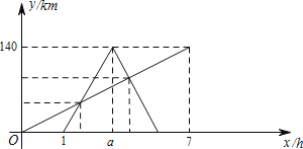
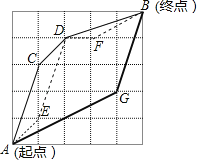
名校课堂系列答案
【题目】嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R1，R2，R3，其行经位置如图与表所示：
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R1、R2、R3这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．
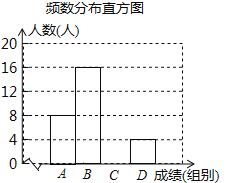
【题目】“品中华诗词，寻文化基因”．某校举办了第二届“中华诗词大赛”，将该校八年级参加竞赛的学生成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图．
频数分布统计表
组别 | 成绩x（分） | 人数 | 百分比 |
A | 60≤x＜70 | 8 | 20% |
B | 70≤x＜80 | 16 | m% |
C | 80≤x＜90 | a | 30% |
D | 90≤＜x≤100 | 4 | 10% |
请观察图表，解答下列问题：
（1）表中a= ，m= ；
（2）补全频数分布直方图；
（3）D组的4名学生中，有1名男生和3名女生．现从中随机抽取2名学生参加市级竞赛，则抽取的2名学生恰好是一名男生和一名女生的概率为 ．
