题目内容
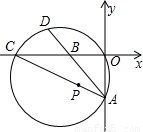
(2000•河南)如图,在直角坐标系内,点B、C在x轴的负半轴上,点A在y轴的负半轴上.以AC为直径的圆与AB的延长线交于点D,弧CD=弧AO,如果AB=10,AO>BO,且AO、BO是x的二次方程x2+kx+48=0的两个根.(1)求点D的坐标;
(2)若点P在直径AC上,且AP=
 AC,判断点(-2,-10)是否在过D、P两点的直线上,并说明理由.
AC,判断点(-2,-10)是否在过D、P两点的直线上,并说明理由.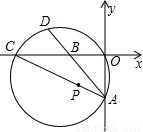
【答案】分析:(1)因为AO、BO是x的二次方程x2+kx+48=0的根,所以利用根与系数的关系可得AO+BO=-k,AO•BO=48.
结合勾股定理,可得AB2=AO2+BO2即100=k2-96,解之可求k=±14,结合已知条件知-k>0,所以k=-14,解方程就可求出AO=8,BO=6.又因AC是直径,所以∠D=∠O=90°,又因弧CD=弧AO,所以CD=AO=8,可证△DBC≌△OBA,得到DB=OB=6,OA=CD=8,CB=AB=10,作DE⊥CO于E,则△DEB∽△AOB,利用相似三角形的对应边的比等于相似比,可求出DE=4.8,BE=3.6,从而求出D(-9.6,4.8).
(2)利用勾股定理求出AC=8 ,则AP=
,则AP= AC=2
AC=2 ,
,
作PF⊥OC于F,则△PCF∽△ACO,所以 ,进而可求出PF=6,CF=12,OF=16-12=4,P(-4,-6),
,进而可求出PF=6,CF=12,OF=16-12=4,P(-4,-6),
再利用待定系数法即可求出PD的解析式.
令x=-2,则y=- 验证,看点(-2,-10)是否在过D、P两点的直线上.
验证,看点(-2,-10)是否在过D、P两点的直线上.
解答:解:(1)∵AO、BO是x的二次方程x2+kx+48=0的根,
∴AO+BO=-k,AO•BO=48,
∵AB=10,∠O=90°,
∴AB2=AO2+BO2,
∴100=k2-96,
∴k=±14,
∵-k>0
∴k=-14,
∴x2-14x+48=0,
∴x=6,x=8,
∵AO>BO,
∴AO=8,BO=6,
∵AC是直径,
∴∠CDA=∠COA=90°,
∵弧CD=弧AO,
∴CD=AO=8.
∵∠DBC=∠OBA,
∴△DBC≌△OBA,
∴DB=OB=6,OA=CD=8,CB=AB=10,
作DE⊥CO于E,则△DEB∽△AOB,
∴
∴
∴DE=4.8,BE=3.6,
∴OE=3.6+6=9.6,D(-9.6,4.8).
(2)∵AD=DB+AB=6+10=16,CD=8,∠ADC=90°,
∴AC=8 ,
,
∴AP= AC=2
AC=2 .
.
作PF⊥OC于F,则△PCF∽△ACO.
∴
∴
∴PF=6,CF=12,OF=16-12=4,
∴P(-4,-6),
又因D(-9.6,4.8),
所以设PD的解析式为y=kx+b,
∴
∴
∴
令x=-2,则y=- .
.
所以点(-2,-10)不在过D、P两点的直线上.
点评:本题需利用待定系数法和相似三角形的性质来解决问题,还考查了用待定系数法求一次函数的解析式,综合性较强,难度比较大.
结合勾股定理,可得AB2=AO2+BO2即100=k2-96,解之可求k=±14,结合已知条件知-k>0,所以k=-14,解方程就可求出AO=8,BO=6.又因AC是直径,所以∠D=∠O=90°,又因弧CD=弧AO,所以CD=AO=8,可证△DBC≌△OBA,得到DB=OB=6,OA=CD=8,CB=AB=10,作DE⊥CO于E,则△DEB∽△AOB,利用相似三角形的对应边的比等于相似比,可求出DE=4.8,BE=3.6,从而求出D(-9.6,4.8).
(2)利用勾股定理求出AC=8
 ,则AP=
,则AP= AC=2
AC=2 ,
,作PF⊥OC于F,则△PCF∽△ACO,所以
 ,进而可求出PF=6,CF=12,OF=16-12=4,P(-4,-6),
,进而可求出PF=6,CF=12,OF=16-12=4,P(-4,-6),再利用待定系数法即可求出PD的解析式.
令x=-2,则y=-
 验证,看点(-2,-10)是否在过D、P两点的直线上.
验证,看点(-2,-10)是否在过D、P两点的直线上.解答:解:(1)∵AO、BO是x的二次方程x2+kx+48=0的根,
∴AO+BO=-k,AO•BO=48,
∵AB=10,∠O=90°,
∴AB2=AO2+BO2,
∴100=k2-96,
∴k=±14,
∵-k>0
∴k=-14,
∴x2-14x+48=0,
∴x=6,x=8,
∵AO>BO,
∴AO=8,BO=6,
∵AC是直径,
∴∠CDA=∠COA=90°,
∵弧CD=弧AO,
∴CD=AO=8.
∵∠DBC=∠OBA,
∴△DBC≌△OBA,

∴DB=OB=6,OA=CD=8,CB=AB=10,
作DE⊥CO于E,则△DEB∽△AOB,
∴

∴

∴DE=4.8,BE=3.6,
∴OE=3.6+6=9.6,D(-9.6,4.8).
(2)∵AD=DB+AB=6+10=16,CD=8,∠ADC=90°,
∴AC=8
 ,
,∴AP=
 AC=2
AC=2 .
.作PF⊥OC于F,则△PCF∽△ACO.
∴

∴

∴PF=6,CF=12,OF=16-12=4,
∴P(-4,-6),
又因D(-9.6,4.8),
所以设PD的解析式为y=kx+b,
∴

∴

∴

令x=-2,则y=-
 .
.所以点(-2,-10)不在过D、P两点的直线上.
点评:本题需利用待定系数法和相似三角形的性质来解决问题,还考查了用待定系数法求一次函数的解析式,综合性较强,难度比较大.

练习册系列答案
相关题目
 AC,判断点(-2,-10)是否在过D、P两点的直线上,并说明理由.
AC,判断点(-2,-10)是否在过D、P两点的直线上,并说明理由.