题目内容
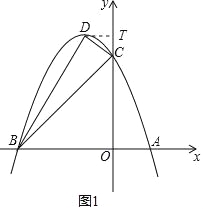
【题目】如图,抛物线y=![]() +bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
+bx+c的对称轴为x=﹣1,该抛物线与x轴交于A、B两点,且A点坐标为(1,0),交y轴于C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并予证明.
(3)在对称轴上是否存在一点P,使得△ACP为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)y=![]() ﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形,理由详见解析;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,
﹣2x+3,顶点D为(﹣1,4);(2)△DCB为直角三角形,理由详见解析;(3) 存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,0)或(﹣1,6).
)或(﹣1,0)或(﹣1,6).
【解析】
试题分析:(1)根据抛物线的对称性得到点B的坐标为(﹣3,0),故设抛物线为两点式方程y=a(x﹣1)(x+3),把点C的坐标代入即可求得a的值;利用配方法将抛物线解析式转化为顶点式,即可得到顶点D的坐标;
(2)过D作DT⊥y轴于T,则可求得∠DCT=45°,∠BCO=45°,则可判断△BCD的形状;
(3)可设出P(﹣1,t),则可分别表示出AP、CP、AC的长度,分AP=CP、AP=AC和CP=AC三种情况分别可得到关于t的方程,可求得P点坐标.
试题解析:(1)点A(1,0)关于x=﹣1的对称点B(﹣3,0),
设过A(1,0)、B(﹣3,0)的抛物线为y=a(x﹣1)(x+3),
该抛物线又过C(0,3),则有:3=﹣3a,解得a=﹣1,
即y=![]() =
=![]() ﹣2x+3,顶点D为(﹣1,4);
﹣2x+3,顶点D为(﹣1,4);
(2)△DCB为直角三角形,理由如下:
过D点,作DT⊥y轴于T,如图1,
则T(0,4).
∵DT=TC=1,
∴△DTC为等腰直角三角形,
∴∠DCT=45°,
同理可证∠BCO=45°,
∴∠DCB=90°,
∴△DCB为直角三角形;
(3)设P(﹣1,t),
∵A(1,0),C(0,3),
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,![]() =
=![]() =10,
=10,
∵△APC为等腰三角形,
∴有AP=CP、AP=AC和CP=AC三种情况,
①当AP=CP时,则有![]() =
=![]() ,即
,即![]() =
=![]() ,解得t=1,此时P(﹣1,1);
,解得t=1,此时P(﹣1,1);
②当AP=AC时,则有![]() =
=![]() ,即
,即![]() =10,解得t=
=10,解得t=![]() ,此时P(﹣1,
,此时P(﹣1,![]() )或(﹣1,
)或(﹣1,![]() );
);
③当CP=AC时,则有![]() =
=![]() ,即
,即![]() =10,解得t=0或t=6,此时P(﹣1,0)或P(﹣1,6);
=10,解得t=0或t=6,此时P(﹣1,0)或P(﹣1,6);
综上可知存在满足条件的点P,其坐标为(﹣1,1)或(﹣1,![]() )或(﹣1,
)或(﹣1,![]() )或(﹣1,0)或(﹣1,6).
)或(﹣1,0)或(﹣1,6).

【题目】学校为了丰富学生课余活动开展了一次“爱我学校,唱我学校”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60B.9.60,9.60C.9.60,9.70D.9.65,9.60
【题目】广州市运动员在最近八届亚运会上获得金牌的运动项目种类及金牌数量如下表所示:
田径 | 羽毛球 | 篮球 | 水球 | 网球 | 台球 | 足球 | 体操 | 游泳 | 举重 | 射击 | 击剑 | 拳击 | 赛艇 | 跳水 |
7 | 8 | 2 | 4 | 2 | 1 | 1 | 3 | 2 | 4 | 4 | 12 | 1 | 5 | 1 |
给出下列说法:①广州市运动员在最近八届亚运会上获得金牌的运动项目共有15个;②广州市运动员在最近八届亚运会上获得金牌的总数是57;③上表中,击剑类的频率约为0.211.其中正确的有( )
A.3个
B.2个
C.1个
D.0个