题目内容
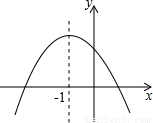
(2002•海南)已知二次函数y= x2-x+m的图象经过点A(-3,6),并与x轴交于B、C两点(点B在C的左边),P为它的顶点.
x2-x+m的图象经过点A(-3,6),并与x轴交于B、C两点(点B在C的左边),P为它的顶点.(1)试确定m的值;
(2)设点D为线段OC上的一点,且满足∠DPC=∠BAC,求直线AD的解析式.
【答案】分析:(1)把点A的坐标代入函数解析式,可以求出m的值.
(2)二次函数的顶点坐标可以根据化简的二次函数式求出,令y=0则代入解析式则可求出与x轴的交点B、C的坐标,易证△AEC是等腰直角三角形,作PF⊥x轴于F,可以证明△DPC∽△BAC,根据相似三角形的对应边的比相等,可以求出D的坐标,根据待定系数法就可以求出直线AD的解析式.
解答: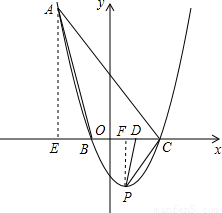 解:(1)把点A的坐标代入函数解析式,得到:6=
解:(1)把点A的坐标代入函数解析式,得到:6= ×(-3)2-(-3)+m,
×(-3)2-(-3)+m,
解得m=- .
.
(2)因为y= x2-x-
x2-x- =
= (x-1)2-2,
(x-1)2-2,
所以顶点坐标是p(1,-2).
令y=0,得 (x-1)2-2=0,
(x-1)2-2=0,
解得x=-1或x=3.
所以抛物线与x轴的交点坐标是B(-1,0),C(3,0)
作AE⊥x轴于E,易知|AE|=|CE|=6,
∴△AEC是等腰直角三角形,
∴∠ACB=45°.
作PF⊥x轴于F,
同理得到∠PCD=45°=∠ACB又因为∠DPC=∠BAC,
∴△DPC∽△BAC.
∴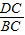 =
=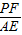 .
.
设点D的坐标是(a,0),
那么DC=3-a,另外BC=4,PF=2,AE=6,
∴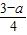 =
= ,
,
解得a=
∴点D的坐标是( ,0).
,0).
设直线AD的解析式为y=kx+b,把点A,D的坐标代入得到: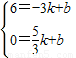 ,
,
解得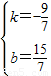 .
.
∴直线AD的解析式是y=- x+
x+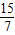 .
.
点评:本题主要考查了二次函数的顶角坐标的求解方法,以及利用待定系数法求函数的解析式.
(2)二次函数的顶点坐标可以根据化简的二次函数式求出,令y=0则代入解析式则可求出与x轴的交点B、C的坐标,易证△AEC是等腰直角三角形,作PF⊥x轴于F,可以证明△DPC∽△BAC,根据相似三角形的对应边的比相等,可以求出D的坐标,根据待定系数法就可以求出直线AD的解析式.
解答:
 解:(1)把点A的坐标代入函数解析式,得到:6=
解:(1)把点A的坐标代入函数解析式,得到:6= ×(-3)2-(-3)+m,
×(-3)2-(-3)+m,解得m=-
 .
.(2)因为y=
 x2-x-
x2-x- =
= (x-1)2-2,
(x-1)2-2,所以顶点坐标是p(1,-2).
令y=0,得
 (x-1)2-2=0,
(x-1)2-2=0,解得x=-1或x=3.
所以抛物线与x轴的交点坐标是B(-1,0),C(3,0)
作AE⊥x轴于E,易知|AE|=|CE|=6,
∴△AEC是等腰直角三角形,
∴∠ACB=45°.
作PF⊥x轴于F,
同理得到∠PCD=45°=∠ACB又因为∠DPC=∠BAC,
∴△DPC∽△BAC.
∴
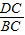 =
=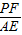 .
.设点D的坐标是(a,0),
那么DC=3-a,另外BC=4,PF=2,AE=6,
∴
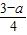 =
= ,
,解得a=

∴点D的坐标是(
 ,0).
,0).设直线AD的解析式为y=kx+b,把点A,D的坐标代入得到:
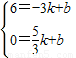 ,
,解得
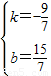 .
.∴直线AD的解析式是y=-
 x+
x+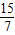 .
.点评:本题主要考查了二次函数的顶角坐标的求解方法,以及利用待定系数法求函数的解析式.

练习册系列答案
相关题目
 x2-x+m的图象经过点A(-3,6),并与x轴交于B、C两点(点B在C的左边),P为它的顶点.
x2-x+m的图象经过点A(-3,6),并与x轴交于B、C两点(点B在C的左边),P为它的顶点.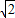 ,则MB的长度为 .
,则MB的长度为 . ,则MB的长度为 .
,则MB的长度为 .