题目内容
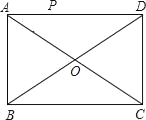
如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )
A. 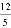 B.
B.  C.
C. 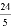 D. 不确定
D. 不确定
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
题目内容
如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )

A. 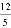 B.
B.  C.
C. 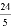 D. 不确定
D. 不确定
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案