题目内容
观察下列各式:
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
……………………
请你把发现的规律用含正整数n的等式表示为 .
1×3+1=4=22
2×4+1=9=32
3×5+1=16=42
4×6+1=25=52
……………………
请你把发现的规律用含正整数n的等式表示为 .
(n-1)(n+1)+1=n2.
试题分析:等式的左边是相差为2的两个数相乘加1,右边是两个数的平均数的平方,由题,∵1×3+1=22;3×5+1=42;5×7+1=62;7×9+1=82,∴规律为:(n-1)(n+1)+1=n2.

练习册系列答案
相关题目
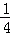 ﹣7.2+|﹣
﹣7.2+|﹣ |.
|. )÷3×(﹣12)﹣42.
)÷3×(﹣12)﹣42.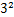 与
与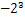
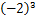
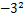 与
与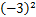
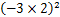 与
与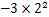
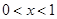 ,则
,则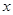 ,
, ,
,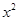 的大小关系是( )
的大小关系是( )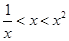
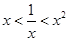
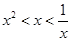

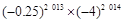 =______.
=______.