题目内容
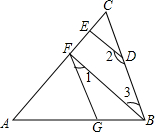 如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,试判断∠AGF与∠ABC的大小关系,并说明理由.
如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,试判断∠AGF与∠ABC的大小关系,并说明理由.分析:由于DE⊥AC,BF⊥AC得到∠AFB=∠AED=90°,由BF∥DE,根据平行线的性质得∠2+∠3=180°,则∠1=∠3,可判断GF∥BC,所以∠AGF=∠ABC.
解答:解:∠AGF=∠ABC.
理由如下:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠AED=90°,
∴BF∥DE,
∴∠2+∠3=180°,
又∵∠1+∠2=180°
∴∠1=∠3,
∴GF∥BC,
∴∠AGF=∠ABC.
理由如下:∵DE⊥AC,BF⊥AC,
∴∠AFB=∠AED=90°,
∴BF∥DE,
∴∠2+∠3=180°,
又∵∠1+∠2=180°
∴∠1=∠3,
∴GF∥BC,
∴∠AGF=∠ABC.
点评:本题考查了平行线的判定与性质:内错角相等,两直线平行;两直线平行,同位角相等,同旁内角互补.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目


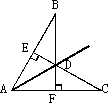
 如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,试判断∠AGF与∠ABC的大小关系,并说明理由.
如图,DE⊥AC于点E,BF⊥AC于点F,∠1+∠2=180°,试判断∠AGF与∠ABC的大小关系,并说明理由.