题目内容
 如图,抛物线过点O(0,0),A(3,3)和B(4,0).
如图,抛物线过点O(0,0),A(3,3)和B(4,0).(1)求抛物线的解析式;
(2)若抛物线的顶点为M,求四边形OMAB的面积.
分析:(1)设抛物线解析式为y=ax2+bx+c,把点O、A、B的坐标代入求解即可;
(2)把抛物线整理成顶点式形式,然后写出顶点坐标,再把四边形OMAB的面积分成两个直角三角形与一个梯形的面积列式进行计算即可得解.
(2)把抛物线整理成顶点式形式,然后写出顶点坐标,再把四边形OMAB的面积分成两个直角三角形与一个梯形的面积列式进行计算即可得解.
解答: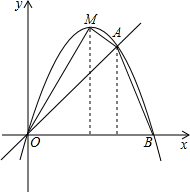 解:(1)设抛物线解析式为y=ax2+bx+c,
解:(1)设抛物线解析式为y=ax2+bx+c,
∵抛物线过点O(0,0),A(3,3)和B(4,0),
∴
,
解得
,
所以,抛物线的解析式为y=-x2+4x;
(2)∵y=-x2+4x=-(x-2)2+4;
∴顶点坐标为(2,4),
四边形OMAB的面积=
×4×2+
×(3+4)×(3-2)+
×(4-3)×3,
=4+
+
,
=9.
 解:(1)设抛物线解析式为y=ax2+bx+c,
解:(1)设抛物线解析式为y=ax2+bx+c,∵抛物线过点O(0,0),A(3,3)和B(4,0),
∴
|
解得
|
所以,抛物线的解析式为y=-x2+4x;
(2)∵y=-x2+4x=-(x-2)2+4;
∴顶点坐标为(2,4),
四边形OMAB的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4+
| 7 |
| 2 |
| 3 |
| 2 |
=9.
点评:本题考查了待定系数法求二次函数解析式,是求函数解析式常用的方法,一定要熟练掌握,(2)把不规则四边形的面积分成常见的图形求面积是常用的方法.

练习册系列答案
相关题目
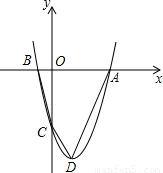
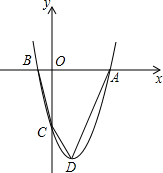 如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程
如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程 如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程
如图,抛物线过点A(x1,0)、B(x2,0)、C(0,-8),x1、x2是方程 x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点.
x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点. S四边形ABCD.
S四边形ABCD.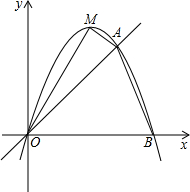 如图,抛物线过点O(0,0),A(3,3)和B(4,0).
如图,抛物线过点O(0,0),A(3,3)和B(4,0). x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点.
x2-x-4=0的两根,且x1>x2,点D是此抛物线的顶点. S四边形ABCD.
S四边形ABCD.