题目内容
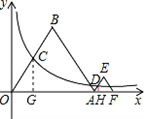
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
 (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.

| 解:(1)过点C作CG⊥OA于点G, ∵点C是等边△OAB的边OB的中点, ∴OC=2,∠ AOB=60°, ∴OG=1,CG= 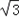 , ,∴点C的坐标是(1, 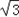 ), ),由 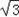 = = ,得:k= ,得:k=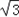 , ,∴该双曲线所表示的函数解析式为y= 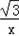 ; ;(2)过点D作DH⊥AF于点H,设AH=a,则DH= 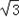 a. a.∴点D的坐标为(4+a, 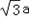 ), ),∵点D是双曲线y= 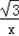 上的点, 上的点,由xy=  ,得 ,得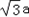 (4+a)= (4+a)=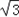 , ,即:a2+4a﹣1=0, 解得:a1= 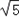 ﹣2,a2=﹣ ﹣2,a2=﹣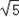 ﹣2(舍去), ﹣2(舍去),∴AD=2AH=2 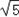 ﹣4, ﹣4,∴等边△AEF的边长是2AD=4 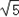 ﹣8. ﹣8. |
 |

练习册系列答案
相关题目
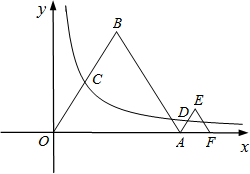 (2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
(2012•丽水)如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4. 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4. 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.