��Ŀ����
����Ŀ��ijó��˾���������������ݴ�ײˣ�����Ϊÿ��20Ԫ����۲��Ź涨�����۵���ÿ�ò��ó���80Ԫ��Ҳ���õ���30Ԫ�������鷢�֣��վ�������y���ã������۵���x��Ԫ/�ã�����һ�κ�����ϵ������ÿ���ۼ�60Ԫʱ���վ�����90�ã�ÿ���ۼ�30Ԫʱ���վ�����120�ã�
��1�����վ�������y�����۵���x�ĺ�����ϵʽ��
��2�������۹����У�ÿ�컹Ҫ֧����������200Ԫ������������w��Ԫ�������۵���x֮��ĺ�����ϵʽ���������۵���Ϊ��ֵʱ���ɻ��������������������������Ƕ��٣�
���𰸡���1��y=��x+150����30��x��80��;(2) ��x=80ʱȡ�����ֵ��ΪW���ֵ=����80��85��2+4025=4000Ԫ��
�������������������1����һ�κ�������ʽΪy=kx+b���ѣ�60��90������30��120���ֱ������ʽ�õ�һ�κ�������ʽ��
��2����������õ�W=��x��20������x+150����200���䷽�������ֵ��
�����������1����һ�κ�������ʽΪ��һ�κ�������ʽΪy=kx+b��
�ѣ�60��90������30��120���ֱ������ʽ�ã� ![]() ��
��
���![]() ��
��
��y=��x+150����30��x��80����
��2�����������W=��x��20������x+150����200
=��x2+170x��3200
=����x2��170x+852��852����3200
=����x��85��2+852��3200
=����x��85��2+852��3200
=����x��85��2+4025��
��x=80ʱȡ�����ֵ��ΪW���ֵ=����80��85��2+4025=4000Ԫ��

 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
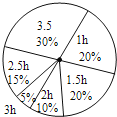
һ����ʦ����Ӧ����������һ��ȫϵ�д�����Ŀ�������꼶ѧϰѹ����ѧ���ڼ���ѧʱ��ϳ�һ����������Ϊ�˽�ѧ��ѧϰʱ�䣬���꼶�����ȡ25%��ѧ���ʾ����飬�Ƴ�ͳ�Ʊ�������ͳ��ͼ���������ͼ�����ṩ����Ϣ�ش��������⣺
ѧϰʱ��(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
���� | 72 | 36 | 54 | 18 |
��1�������꼶����ѧ��_____����
��2���ڱ����еĿո�������Ӧ��������
��3�����������ṩ��ѧ��ѧϰʱ�����λ����_____��������_____��