题目内容
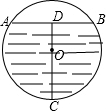如图是一个装有水的水管的截面，已知水管的直径是100cm，装有水的液面宽度为AB=60cm，CD为过圆心且CD⊥AB，则水管中水的最大深度为多少？
分析：首先连接OA，根据题意可得CD⊥AB，然后由垂径定理，即可求得AD的长，在Rt△AOD中，利用勾股定理，即可求得OD的长，继而求得水管中水的最大深度．
解答：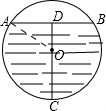
解：连接OA，
根据题意得：CD⊥AB，
∴AD=
AB=
×60=30（cm），
∵水管的直径是100cm，
∴OA=50cm，
在Rt△AOD中，OD=
=40（cm），
∴CD=OC+OD=90（cm）．
∴水管中水的最大深度为90cm．
解：连接OA，根据题意得：CD⊥AB，
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵水管的直径是100cm，
∴OA=50cm，
在Rt△AOD中，OD=
| OA2-AD2 |
∴CD=OC+OD=90（cm）．
∴水管中水的最大深度为90cm．
点评：此题考查了垂径定理的应用．题目比较简单，解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
（2013•孝感）如图，一个装有进水管和出水管的容器，从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，接着关闭进水管直到容器内的水放完．假设每分钟的进水量和出水量是两个常数，容器内的水量y（单位：升）与时间x（单位：分）之间的部分关系．那么，从关闭进水管起
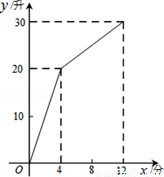
如图是一个装有水的水管的截面，已知水管的直径是100cm，装有水的液面宽度为AB=60cm，则水管中水的最大深度为多少？