Question

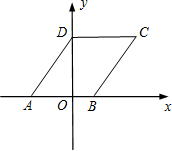（2012•高淳县二模）如图，四边形ABCD为菱形，已知A（-3，0），B（2，0），则点C的坐标为

（5，4）

．

Answer 1

分析：先根据点A、B的坐标求出AB的长度，再根据菱形的四条边都相等求出AD、CD的长度，再利用勾股定理求出OD的长度，然后即可得解．

解答：解：∵A（-3，0），B（2，0），
∴AB=2-（-3）=2+3=5，AO=3，
∵四边形ABCD为菱形，
∴AD=CD=AB=5，
在Rt△AOD中，OD=

AD2-AO2

=

52-32

=4，
故点C（5，4）．
故答案为：（5，4）．

点评：本题考查了菱形的四条边都相等的性质，勾股定理的应用，是基础题，比较简单．