题目内容
【题目】我们知道多项式的乘法可以利用图形的面积进行解释,例如,(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示:
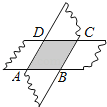
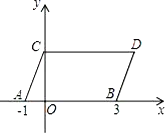
(1)请你写出图3所表示的一个等式: .
(2)试画出一个图形,使它的面积能表示成(a+b)(a+3b)=a2+4ab+3b2.
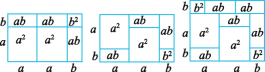
图1 图2 图3
【答案】(1)(a+2b)(2a+b)=2a2+5ab+2b2 (2)见解析
【解析】
试题(1)由题意得:长方形的面积=长×宽,即可将长和宽的表达式代入,再进行多项式的乘法,即可得出等式;
(2)已知图形面积的表达式,即可根据表达式得出图形的长和宽的表达式,即可画出图形.
解:(1)∵长方形的面积=长×宽,
∴图3的面积=(a+2b)(2a+b)=2a2+5ab+2b2,
故图3所表示的一个等式:(a+2b)(2a+b)=2a2+5ab+2b2,
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)∵图形面积为:(a+b)(a+3b)=a2+4ab+3b2,
∴长方形的面积=长×宽=(a+b)(a+3b),
由此可画出的图形为:


练习册系列答案
相关题目