题目内容
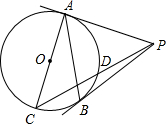如图，PA、PB与⊙O分别相切于点A、点B，AC是⊙O的直径，PC交⊙O于点D，已知∠APB=60°，AC=2，那么CD的长为分析：连接AD，OB，OP，根据已知可求得AP，PC的长，再根据切割线定理得，PA2=PD•PC，从而可求得PD与CD的长．
解答：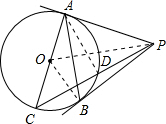
解：连接AD，OB，OP；
∵PA、PB与⊙O分别相切于点A、点B，
∴∠OAP=∠OBP=90°，∠AOB=180°-∠P=120°，
∴∠AOP=60°，AP=AOtan60°=
，
∴PC=
；
∵PA2=PD•PC，
∴PD=
，
∴CD=
．
解：连接AD，OB，OP；∵PA、PB与⊙O分别相切于点A、点B，
∴∠OAP=∠OBP=90°，∠AOB=180°-∠P=120°，
∴∠AOP=60°，AP=AOtan60°=
| 3 |
∴PC=
| 7 |
∵PA2=PD•PC，
∴PD=
3
| ||
| 7 |
∴CD=
4
| ||
| 7 |
点评：本题考查切线的性质，勾股定理，四边形的内角和为360°，切割线定理等的综合运用．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
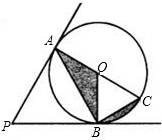如图，PA、PB与⊙O相切，切点分别为A、B，PA=3，∠P=60°，若AC为⊙O的直径，则图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
| D、π |
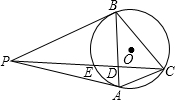如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D．
如图，PA、PB与⊙O相切，切点分别为A、B．PA=3，∠P=60°，若AC为⊙O的直径，则圆中阴影部分的面积为
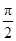B．
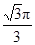D．