题目内容
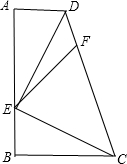 如图八年级“探索”小家庭在一次活动中对一块梯形绿地进行了测量,测量的结果为:
如图八年级“探索”小家庭在一次活动中对一块梯形绿地进行了测量,测量的结果为:(1)AD∥BC;
(2)AD=BE=7m,AE=BC=24m,ED=25m;
(3)4DF=FC.
请你根据测量结果回答下列问题:
(1)EC和ED是否相等?请说明理由.
(2)△EDF的面积为多少?
分析:(1)EC和ED相等,只要证明△AED≌△BCE,根据全等三角形的对应边相等即可求证;
(2)可以证明△DEC是直角三角形,根据三角形的面积公式即可求解.
(2)可以证明△DEC是直角三角形,根据三角形的面积公式即可求解.
解答:解:(1)EC和ED相等
∵AD2+AE2=72+242=252=ED2
∴∠A=90°(1分)
∵AD∥BC
∴∠A=∠B=90°(2分)
∵AD=BE AE=BC
∴△AED≌△BCE(3分)
∴EC=ED(4分)
(2)∵△AED≌△BCE
∴∠AED=∠BCE(1分)
∵∠BEC+∠BCE=90°
∴∠BEC+∠AED=90°
∠DEC=90°(2分)
△DEC的面积=
=
m2(3分)
∵4DF=FC
∴△EDF的面积=
×
=
m2(4分)
∵AD2+AE2=72+242=252=ED2
∴∠A=90°(1分)
∵AD∥BC
∴∠A=∠B=90°(2分)
∵AD=BE AE=BC
∴△AED≌△BCE(3分)
∴EC=ED(4分)
(2)∵△AED≌△BCE
∴∠AED=∠BCE(1分)
∵∠BEC+∠BCE=90°
∴∠BEC+∠AED=90°
∠DEC=90°(2分)
△DEC的面积=
| EC×ED |
| 2 |
| 625 |
| 2 |
∵4DF=FC
∴△EDF的面积=
| 1 |
| 5 |
| 625 |
| 2 |
| 125 |
| 2 |
点评:本题主要考查了三角形全等的判定,证明线段相等的问题常用的方法就是转化为证明三角形全等.

练习册系列答案
相关题目