题目内容
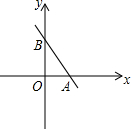 (2012•钦州)如图,直线y=-
(2012•钦州)如图,直线y=-| 3 | 2 |
(-1,-2)或(5,2)
(-1,-2)或(5,2)
.分析:根据直线解析式求出点A、B的坐标,从而得到OA、OB的长度,再根据旋转性质可得△AOB≌△AO′B′,根据全等三角形对应边相等可得AO′、O′B′的长度,然后分顺时针旋转与逆时针旋转两种情况解答.
解答: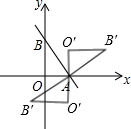 解:当y=0时,-
解:当y=0时,-
x+3=0,解得x=2,
当x=0时,y=3,
所以,点A(2,0),B(0,3),
所以,OA=2,OB=3,
根据旋转不变性可得△AOB≌△AO′B′,
∴AO′=OA=2,O′B′=OB=3,
①如果△AOB是逆时针旋转90°,则点B′(-1,-2),
②如果△AOB是顺时针旋转90°,则点B′(5,2),
综上,点B′的坐标是(-1,-2)或(5,2).
故答案为:(-1,-2)或(5,2).
 解:当y=0时,-
解:当y=0时,-| 3 |
| 2 |
当x=0时,y=3,
所以,点A(2,0),B(0,3),
所以,OA=2,OB=3,
根据旋转不变性可得△AOB≌△AO′B′,
∴AO′=OA=2,O′B′=OB=3,
①如果△AOB是逆时针旋转90°,则点B′(-1,-2),
②如果△AOB是顺时针旋转90°,则点B′(5,2),
综上,点B′的坐标是(-1,-2)或(5,2).
故答案为:(-1,-2)或(5,2).
点评:本题考查了坐标与图形的变化-旋转,根据旋转变换只改变图形的位置不改变图形的性质与 大小求解是解题的关键,注意要分顺时针旋转与逆时针旋转两种情况解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

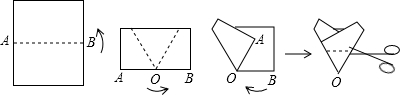
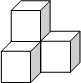 (2012•钦州)如图是由4个小正方体组成的立体图形,它的主视图是( )
(2012•钦州)如图是由4个小正方体组成的立体图形,它的主视图是( )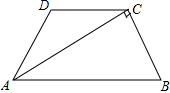 (2012•钦州)如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,BC=8,则等腰梯形ABCD的周长为
(2012•钦州)如图,在等腰梯形ABCD中,AB∥CD,AC⊥BC,∠B=60°,BC=8,则等腰梯形ABCD的周长为