题目内容
 如图所示,各圆两两相切,⊙O半径为2r,⊙A、⊙B半径为r,则⊙C半径为
如图所示,各圆两两相切,⊙O半径为2r,⊙A、⊙B半径为r,则⊙C半径为考点:相切两圆的性质
专题:计算题
分析:首先连接OC,AC,设⊙C半径为x,由各圆两两相切,⊙O半径为2r,⊙A、⊙B半径为r,可得CO⊥AB,OA=r,AC=r+x,OC=2r-x,则可得方程:r2+(2r-x)2=(r+x)2,解此方程即可求得答案.
解答: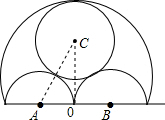 解:连接OC,AC,
解:连接OC,AC,
设⊙C半径为x,
∵各圆两两相切,⊙O半径为2r,⊙A、⊙B半径为r,
∴CO⊥AB,OA=r,AC=r+x,OC=2r-x,
∵OA2+OC2=AC2,
∴r2+(2r-x)2=(r+x)2,
解得:x=
r.
即⊙C半径为:
r.
故答案为:
r.
 解:连接OC,AC,
解:连接OC,AC,设⊙C半径为x,
∵各圆两两相切,⊙O半径为2r,⊙A、⊙B半径为r,
∴CO⊥AB,OA=r,AC=r+x,OC=2r-x,
∵OA2+OC2=AC2,
∴r2+(2r-x)2=(r+x)2,
解得:x=
| 2 |
| 3 |
即⊙C半径为:
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题考查了相切两圆的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目