题目内容
某家庭装饰厨房需用480块某品牌的同一种规格的瓷砖,装饰材料商场出售的这种瓷砖有大、小两种包装,大包装每包50片,价格为30元;小包装每包30片,价格为20元,若大、小包装均不拆开零售,那么怎样制定购买方案才能使所付费用最少?
.解:根据题意,可有三种购买方案;
方案一:只买大包装,则需买包数为: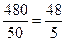 ;
;
由于不拆包零卖.所以需买10包.所付费用为30×10=300(元) … (1分)
方案二:只买小包装.则需买包数为: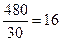
所以需买1 6包,所付费用为1 6×20=320(元) ……… (2分)
方案三:既买大包装.又买小包装,并设买大包装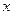 包.小包装
包.小包装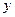 包.所需费用为W元。
包.所需费用为W元。
则 …………(4分)
…………(4分) …………(5分)
…………(5分)
∵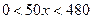 ,且
,且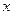 为正整数,
为正整数,
∴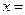 9时,
9时, 290(元).
290(元).
∴购买9包大包装瓷砖和l包小包装瓷砖时,所付费用最少.为290元。
………………………………………………………………(7分)
答:购买9包大包装瓷砖和l包小包装瓷砖时,所付费用最少为290
解析

练习册系列答案
相关题目