题目内容
 如图,AD是角平分线,DE⊥AB于E,DF⊥AC于F,连接EF交AD于G,则下列结论:
如图,AD是角平分线,DE⊥AB于E,DF⊥AC于F,连接EF交AD于G,则下列结论:
①AE=AF; ②EG=GF; ③AD⊥EF; ④BE=DE.其中正确的是
- A.①③④
- B.②③④
- C.①②④
- D.①②③
D
分析:根据角平分线的性质,得DE=DF,根据线段垂直平分线性质定理的逆定理,得点D在EF的垂直平分线上;根据等角对等边,AE=AF,则点A在EF的垂直平分线上,从而可证得AD⊥EF;又因为AE=AF,AG共线,AD是角平分线,从而可根据SAS证明△AEG≌△AFG,则有EG=GF.
解答:∵AD为△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴点D在EF的垂直平分线上,∠DEF=∠DFE,
∵∠DEA=∠DFA=90°,
∴∠FEA=∠EFA,
∴AE=AF,故①正确;
∴点A在EF的垂直平分线上,
∴AD⊥EF,故③正确;
∵AE=AF,∠EAG=∠FAG,AG=AG,
∴△AEG≌△AFG,
∴EG=GF,故②正确.
故选D.
点评:此题主要是综合运用了角平分线的性质定理和线段垂直平分线性质定理的逆定理.
分析:根据角平分线的性质,得DE=DF,根据线段垂直平分线性质定理的逆定理,得点D在EF的垂直平分线上;根据等角对等边,AE=AF,则点A在EF的垂直平分线上,从而可证得AD⊥EF;又因为AE=AF,AG共线,AD是角平分线,从而可根据SAS证明△AEG≌△AFG,则有EG=GF.
解答:∵AD为△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∴点D在EF的垂直平分线上,∠DEF=∠DFE,
∵∠DEA=∠DFA=90°,
∴∠FEA=∠EFA,
∴AE=AF,故①正确;
∴点A在EF的垂直平分线上,
∴AD⊥EF,故③正确;
∵AE=AF,∠EAG=∠FAG,AG=AG,
∴△AEG≌△AFG,
∴EG=GF,故②正确.
故选D.
点评:此题主要是综合运用了角平分线的性质定理和线段垂直平分线性质定理的逆定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 3、如图,△ABC中,AB=AC,AD是角平分线,DE⊥AB,DF⊥AC,E、F为垂足,对于结论:①DE=DF;②BD=CD;③AD上任一点到AB、AC的距离相等;④AD上任一点到B、C的距离相等.其中正确的是( )
3、如图,△ABC中,AB=AC,AD是角平分线,DE⊥AB,DF⊥AC,E、F为垂足,对于结论:①DE=DF;②BD=CD;③AD上任一点到AB、AC的距离相等;④AD上任一点到B、C的距离相等.其中正确的是( )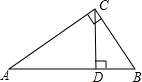 (1)如图,CD是Rt△ABC斜边上的高,AC=4,BC=3.则cos∠BCD的值是
(1)如图,CD是Rt△ABC斜边上的高,AC=4,BC=3.则cos∠BCD的值是 25、如图,在△ABC中,∠ACB=90°,AD是角平分线,CH是高,交AD于F,DE⊥AB于E,试证明四边形CDEF是菱形.
25、如图,在△ABC中,∠ACB=90°,AD是角平分线,CH是高,交AD于F,DE⊥AB于E,试证明四边形CDEF是菱形. 7、如图,AD是角平分线,DE⊥AB于E,DF⊥AC于F,连接EF交AD于G,则下列结论:
7、如图,AD是角平分线,DE⊥AB于E,DF⊥AC于F,连接EF交AD于G,则下列结论: