题目内容
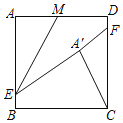
【题目】如图所示,正方形ABCD中,AB=8,BE=DF=1,M是射线AD上的动点,点A关于直线EM的对称点为A′,当△A′FC为以FC为直角边的直角三角形时,对应的MA的长为___________.
【答案】![]() 或
或![]()
【解析】
由正方形的性质可得AB=CD=8,∠D=∠C=90°,由折叠的性质可得AE=A'E=7,AM=A'M,∠A=∠EA'M=90°,分两种情况讨论,由相似三角形的性质可求MA的长.
如图,若∠FCA'=90°,即点A'在BC上,过点M作MN⊥BC于点N,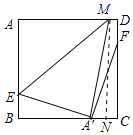
∵四边形ABCD是正方形,
∴AB=CD=8,∠D=∠C=90°,且MN⊥BC
∴四边形MNCD是矩形
∴MN=CD=8
∵AB=8,BE=DF=1,
∴AE=CF=7
∵点A关于直线EM的对称点为A′,
∴AE=A'E=7,AM=A'M,∠A=∠EA'M=90°
∴A'B=![]() ,
,
∵∠BA'E+∠MA'N=90°,∠BA'E+∠A'EB=90°,
∴∠BEA'=∠MA'N,且∠B=∠MNA'=90°
∴△A'BE∽△MNA',
∴![]() ,
,
∴![]()
∴A'M=![]()
如图,若∠A'FC=90°,过点A'作HG⊥AD,过点E作EN⊥HG,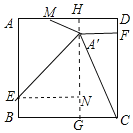
∵四边形ABCD是正方形,
∴AB=CD=8,∠D=∠C=90°,且HG⊥AD
∴四边形HGCD是矩形
∴HG=CD=8,
同理可得NG=BE=1,DF=A'H=1,AE=HN
∵AB=8,BE=DF=1,
∴AE=CF=7
∵点A关于直线EM的对称点为A′,
∴AE=A'E=7=HN,AM=A'M,∠A=∠EA'M=90°
∴A'N=HN-A'H=6
∴EN=![]() ,
,
∵∠NA'E+∠MA'H=90°,∠NA'E+∠A'EN=90°,
∴∠NEA'=∠MA'H,且∠ENA'=∠MHA'=90°
∴△A'NE∽△MHA',
∴![]() ,
,
∴![]()
∴A'M=![]() ,
,
故答案为:![]() 或
或![]()

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案