题目内容
测量底部可以到达的山高AB,可选择与B点在同侧同一直线上的两点C,D,测得CD=50米,在C点测得山顶A的仰角为45°,在D点测得山顶A的仰角为30°,则山高AB等于
- A.50(
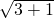 )米
)米 - B.25(
 +1)米
+1)米 - C.25(
 -1)米
-1)米 - D.50(
 -1)米
-1)米
B
分析:易判断出△ABC的形状为等腰直角三角形,利用30°的正切值即可求得山高AB.
解答:设AB=a.
∵∠BCA=45°,
∴BC=a.
∵tan∠ADB=AB:BD,
∴tan30°=a:(a+50).
∴a=25( +1),
+1),
即AB=25( +1)米.
+1)米.
故选B.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.
分析:易判断出△ABC的形状为等腰直角三角形,利用30°的正切值即可求得山高AB.
解答:设AB=a.
∵∠BCA=45°,
∴BC=a.
∵tan∠ADB=AB:BD,
∴tan30°=a:(a+50).
∴a=25(
 +1),
+1),即AB=25(
 +1)米.
+1)米.故选B.
点评:本题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
测量底部可以到达的山高AB,可选择与B点在同侧同一直线上的两点C,D,测得CD=50米,在C点测得山顶A的仰角为45°,在D点测得山顶A的仰角为30°,则山高AB等于( )
A、50(
| ||
B、25(
| ||
C、25(
| ||
D、50(
|
 )米
)米 +1)米
+1)米 -1)米
-1)米 -1)米
-1)米