题目内容
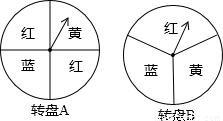
小英和小强做一个“配色”的游戏．下图是两个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色．同时转动两个转盘，如果转盘A转出了红色，转盘B转出了蓝色，或者转盘A转出了蓝色，转盘B转出了红色，则红色和蓝色在一起配成紫色，这种情况下小英获胜；同样，蓝色和黄色在一起配成绿色，这种情况下小强获胜；在其它情况下，则小英、小强不分胜负．
（1）利用列表或树状图的方法表示此游戏所有可能出现的结果；
（2）此游戏的规则，对双方都公平吗？如果公平，请说明理由；如果不公平，请修改游戏规则，使得游戏对双方都公平．
解：（1）用列表法将所有可能出现的结果表示如下：所有可能出现的结果共有12种．
（2）不公平．
上面等可能出现的12种结果中，有3种情况可能得到紫色，故配成紫色的概率是
，即小英获胜的概率是
；但只有2种情况才可能得到绿色，配成绿色的概率是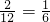
，即小强获胜的概率是
．而
，故小英获胜的可能性大，这个“配色”游戏对双方是不公平的．
修改后的规则：如，红色和蓝色在一起配成紫色，这种情况下小英获胜，红色和黄色在一起配成橙色，这种情况下小强获胜，此时双方获胜的概率都是．
分析：（1）根据题意，用列表法将所有可能出现的结果，即可得答案；
（2）由（1）的表格，分析可能得到紫色、绿色的概率，得到结论；若不公平，根据题意，修改游戏规则即可．
点评：本题考查的是游戏公平性的判断．实际考查概率的计算与游戏公平性的理解，要求学生根据题意，结合实际情况，计算并比较游戏者的胜利的概率，进而得到结论．用到的知识点为：概率=所求情况数与总情况数之比．
| 红 | （红，红） | （蓝，红） | （黄，红） |
| 蓝 | （红，蓝） | （蓝，蓝） | （黄，蓝） |
| 红 | （红，红） | （蓝，红） | （黄，红） |
| 黄 | （红，黄） | （蓝，黄） | （黄，黄） |
| 红 | 蓝 | 黄 |
上面等可能出现的12种结果中，有3种情况可能得到紫色，故配成紫色的概率是
，即小英获胜的概率是；但只有2种情况才可能得到绿色，配成绿色的概率是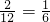，即小强获胜的概率是．而，故小英获胜的可能性大，这个“配色”游戏对双方是不公平的．修改后的规则：如，红色和蓝色在一起配成紫色，这种情况下小英获胜，红色和黄色在一起配成橙色，这种情况下小强获胜，此时双方获胜的概率都是
．分析：（1）根据题意，用列表法将所有可能出现的结果，即可得答案；
（2）由（1）的表格，分析可能得到紫色、绿色的概率，得到结论；若不公平，根据题意，修改游戏规则即可．
点评：本题考查的是游戏公平性的判断．实际考查概率的计算与游戏公平性的理解，要求学生根据题意，结合实际情况，计算并比较游戏者的胜利的概率，进而得到结论．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
