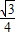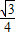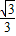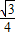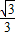题目内容
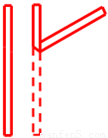
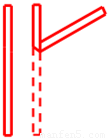
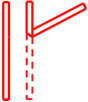 同学们都喜欢老师给他的作业打“红勾”,我们将一张长10cm,宽1cm的矩形红纸条(如左图)进行翻折,便可得到一个漂亮的“红勾”(如右图).如果“红勾”所成的锐角为60°,则这个“红勾”的面积为
同学们都喜欢老师给他的作业打“红勾”,我们将一张长10cm,宽1cm的矩形红纸条(如左图)进行翻折,便可得到一个漂亮的“红勾”(如右图).如果“红勾”所成的锐角为60°,则这个“红勾”的面积为(10-
)
| ||
| 3 |
(10-
)
cm2(结果保留根号).
| ||
| 3 |
分析:根据翻折变换的特点和题意可知,红勾重合的部分正好是个等边三角形,求出它的边长,然后求面积.
解答:解:根据翻折变换的特点和题意可知,
红勾重合的部分正好是个等边三角形,其高是1,
所以它的边长是
,
故等边三角形的面积是
,
所以这个“红勾”的面积为(10-
)cm2.
故答案是:(10-
).
红勾重合的部分正好是个等边三角形,其高是1,
所以它的边长是
2
| ||
| 3 |
故等边三角形的面积是
| ||
| 3 |
所以这个“红勾”的面积为(10-
| ||
| 3 |
故答案是:(10-
| ||
| 3 |
点评:本题考查图形的翻折变换,和等边三角形性质的运用.解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
相关题目
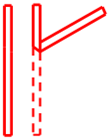 同学们都喜欢老师给他的作业打“红勾”,我们将一张长10cm,宽1cm的矩形红纸条(如左图)进行翻折,便可得到一个漂亮的“红勾”(如图).如果“红勾”所成的锐角为60°,则这个“红勾”的面积为( )cm2.
同学们都喜欢老师给他的作业打“红勾”,我们将一张长10cm,宽1cm的矩形红纸条(如左图)进行翻折,便可得到一个漂亮的“红勾”(如图).如果“红勾”所成的锐角为60°,则这个“红勾”的面积为( )cm2.