Question

某工艺品由一个底面朝上的圆锥体上方嵌入一圆球组成，其横截面如图所示，已知圆锥的母线AB、AC和球体相切，且与底座夹角均为75°，圆锥体底面的周长为20πcm，求球体的半径（参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，结果精确到0.1）

Answer 1

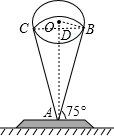解：连接BC，OB，连接OA交BC于点D，
∵圆锥的母线AB、AC和球体相切，
∴OB⊥AB于点B，
∵AB、AC和与底座夹角均为75°，
∴∠BAO=∠BOC=×30°=15°
∵圆锥体底面的周长为20πcm，
∴BD=20π÷2π=10
∴OB=BD÷cos15°=10÷0.97≈10.3cm．
故球体的半径约为10.3cm．
分析：连接BC，OB，连接OA交BC于点D，首先利用圆锥的底面周长求得线段BC的长，然后求得半径OB的长即可．
点评：本题考查了圆锥的计算及切线的性质，解题的关键是通过作辅助线构造直角三角形并求解．