题目内容
 (1)请你任意写出五个正的真分数:
(1)请你任意写出五个正的真分数:(2)比较原来每个分数与对应新分数的大小,可以得出下面的结论:一个真分数是
| a |
| b |
| a+m |
| b+m |
| a+m |
| b+m |
| a |
| b |
(3)请你用文字叙述(2)中结论的含义:
(4)你能用图形的面积说明这个结论吗?
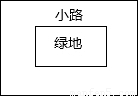
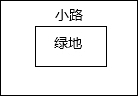
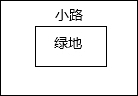
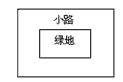
(5)解决问题:如图所示,有一个长宽不等的长方形绿地,现给绿地四周铺一条宽相等的小路,原来的绿地与现在铺过小路后的绿地的长与宽的比值是否相等?为什么?
(6)这个结论可以解释生活中的许多现象,解决许多生活与数学中的问题.请你再提出一个类似的数学问题,或举出一个生活中与此结论相关的例子.
分析:(1)按题目要求进行解答即可.
(2)由(1)的结论可得到
>
;可通过作差法来证明:
令
-
=
,由于b-a>0,所以
>0,因此上述结论是成立的.
(3)可表述为:给一正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数.
(4)可作出三个矩形,边长分别为:a、b,a、m,m、b;然后用a、b、m分别表示出三个矩形的面积,根据它们的面积关系来判断(2)的结论是否正确.
(5)由于绿地的形状是长方形,即长、宽不相等,若长、宽同时加上相同的正数,根据(2)的结论可知长和宽的比值会改变.
(6)此题的答案不唯一,如a>b,即
是假分数时,结论是否有变化等.
(2)由(1)的结论可得到
| a+m |
| b+m |
| a |
| b |
令
| a+m |
| b+m |
| a |
| b |
| m(b-a) |
| b(b+m) |
| m(b-a) |
| b(b+m) |
(3)可表述为:给一正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数.
(4)可作出三个矩形,边长分别为:a、b,a、m,m、b;然后用a、b、m分别表示出三个矩形的面积,根据它们的面积关系来判断(2)的结论是否正确.
(5)由于绿地的形状是长方形,即长、宽不相等,若长、宽同时加上相同的正数,根据(2)的结论可知长和宽的比值会改变.
(6)此题的答案不唯一,如a>b,即
| a |
| b |
解答:解:(1)
、
、
、
、
,
、
、
、
、
.(答案不唯一,符合要求即可)
(2)
>
;
(3)给一正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数;
(4)如图所示,由a<b,得S+S1>S+S2,可以推出:
>
.
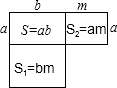
(5)两块绿地的长与宽的比值不相等.
理由:设长方形的绿地的宽和长分别为a、b,且a<b,若铺设的路宽为m,
则铺过小路后的宽和长分别为:a+m、b+m,由(2)的结论知:
<
;
显然比值是不相等的.
(6)数学问题举例:
①若
是假分数,会有怎样的结论?
②a、b不是正数,或不全为正数,情况如何?(答案不唯一)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 8 |
| 1 |
| 9 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 9 |
| 1 |
| 5 |
(2)
| a+m |
| b+m |
| a |
| b |
(3)给一正的真分数的分子、分母同加一个正数,得到的新分数大于原来的分数;
(4)如图所示,由a<b,得S+S1>S+S2,可以推出:
| a+m |
| b+m |
| a |
| b |
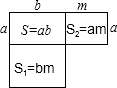
(5)两块绿地的长与宽的比值不相等.
理由:设长方形的绿地的宽和长分别为a、b,且a<b,若铺设的路宽为m,
则铺过小路后的宽和长分别为:a+m、b+m,由(2)的结论知:
| a |
| b |
| a+m |
| b+m |
显然比值是不相等的.
(6)数学问题举例:
①若
| a |
| b |
②a、b不是正数,或不全为正数,情况如何?(答案不唯一)
点评:此题实际考查的是分式的混合运算,熟练掌握分式的基本性质是解题的关键.

练习册系列答案
相关题目
 (1)请你任意写出五个正的真分数:______、______、______、______、______.请给每个分数的分子和分母同加上一个正数得到五个新分数:______、______、______、______、______.
(1)请你任意写出五个正的真分数:______、______、______、______、______.请给每个分数的分子和分母同加上一个正数得到五个新分数:______、______、______、______、______. (a、b均为正数,a<b)给其分子、分母同加上一个正数m,得
(a、b均为正数,a<b)给其分子、分母同加上一个正数m,得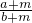 ,则两个分数的大小关系是:
,则两个分数的大小关系是: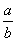 (a、b均为正数,a<b)给其分子.分母同加上一个正数m,得
(a、b均为正数,a<b)给其分子.分母同加上一个正数m,得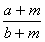 ,则两个分数的大小关系是:
,则两个分数的大小关系是: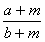 ( )
( )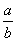 。
。 
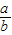 (a、b均为正数,a<b)给其分子、分母同加上一个正数m,得
(a、b均为正数,a<b)给其分子、分母同加上一个正数m,得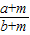 ,则两个分数的大小关系是:
,则两个分数的大小关系是: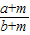 ______
______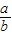 .
.