题目内容
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F. 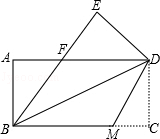
(1)求证:△ABF≌△EDF;
(2)若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
【答案】
(1)证明:由折叠可知,CD=ED,∠E=∠C.
在矩形ABCD中,AB=CD,∠A=∠C.
∴AB=ED,∠A=∠E.
∵∠AFB=∠EFD,
∴△AFB≌△EFD
(2)解:四边形BMDF是菱形.
理由:由折叠可知:BF=BM,DF=DM.
由(1)知△AFB≌△EFD,∴BF=DF.
∴BM=BF=DF=DM.
∴四边形BMDF是菱形
【解析】(1)因为△BCD关于BD折叠得到△BED,显然△BCD≌△BED,得出CD=DE=AB,∠E=∠C=∠A=90°.再加上一对对顶角相等,可证出△ABF≌△EDF;(2)利用折叠知识及菱形的判定可得出四边形BMDF是菱形.

练习册系列答案
相关题目
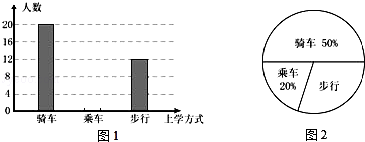
【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级 | 人数/名 |
优秀 | a |
良好 | b |
及格 | 150 |
不及格 | 50 |
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.