Question

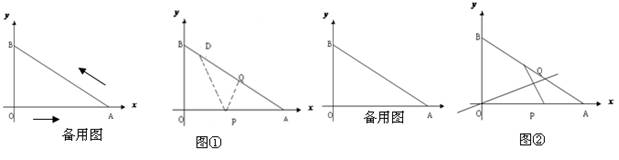
23、已知：如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC=CD，BE⊥CD，垂足为点E，点F在BD上，连接AF、EF．
（1）求证：AD=ED；
（2）如果AF∥CD，求证：四边形ADEF是菱形．

Answer 1

分析：（1）先根据平行的性质得到∠ADB=∠CDB，然后结合BC=CD利用ASA可证得△ABD≌△EBD，继而可得出结论；
（2）根据有一组邻边相等的平行四边形是菱形即可得出结论．

解答：证明：（1）∵BC=CD，
∴∠CDB=∠CBD，
∵AD∥BC，
∴∠ADB=∠CBD，
∴∠ADB=∠CDB，
又∵AB⊥AD，BE⊥CD，
∴∠BAD=∠BED=90°，
于是，在△ABD和△EBD中，
∵∠ADB=∠CDB，∠BAD=∠BED，BD=BD，
∴△ABD≌△EBD，
∴AD=ED．
（2）∵AF∥CD，∴∠AFD=∠EDF，
∴∠AFD=∠ADF，即得AF=AD，
又∵AD=ED，
∴AF=DE，于是，由AF∥DE，AF=DE得四边形ADEF是平行四边形，
又∵AD=ED，
∴四边形ADEF是菱形．

点评：本题考查直角梯形的知识，解答此题的关键是根据平行和直角三角形的性质找出图中的相似三角形，利用相似三角形的性质解答此题．