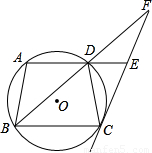
题目内容
（2005•临沂）如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E，若AD=5，AB=6，BC=9．（1）求DC的长；
（2）求证：四边形ABCE是平行四边形．
【答案】分析：（1）∵AD∥BC，∴AB=DC=6；
（2）可先证△CDE∽△BCD，求得DE=4，可得AE=9，∴AE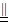
BC∴四边形ABCE是平行四边形．
解答：（1）解：∵AD∥BC
∴AB=DC
∴DC=AB=6（2分）
（2）证明：∵AD∥BC，
∴∠EDC=∠BCD
又∵PC与⊙O相切
∴∠ECD=∠DBC
∴△CDE∽△BCD（4分）
∴
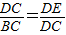
∴DE=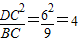
（6分）
∴AE=AD+DE=5+4=9（7分）
∴AE
BC
∴四边形ABCE是平行四边形．（9分）
点评：此题主要考查平行四边形的判定，综合利用了切线和相似三角形的性质．
（2）可先证△CDE∽△BCD，求得DE=4，可得AE=9，∴AE
BC∴四边形ABCE是平行四边形．解答：（1）解：∵AD∥BC
∴AB=DC
∴DC=AB=6（2分）
（2）证明：∵AD∥BC，
∴∠EDC=∠BCD
又∵PC与⊙O相切
∴∠ECD=∠DBC
∴△CDE∽△BCD（4分）
∴
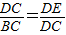
∴DE=
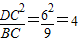（6分）∴AE=AD+DE=5+4=9（7分）
∴AE
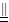BC∴四边形ABCE是平行四边形．（9分）
点评：此题主要考查平行四边形的判定，综合利用了切线和相似三角形的性质．
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
