题目内容
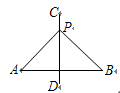
如图,直线 是一条河,
是一条河, 两地相距8千米,
两地相距8千米, 两地到
两地到 的距离分别为2千米,5千米,欲在
的距离分别为2千米,5千米,欲在 上的某点
上的某点 处修建一个水泵站,向
处修建一个水泵站,向 两地供水.现有如下四种铺设方案,则铺设的管道最短的是( )
两地供水.现有如下四种铺设方案,则铺设的管道最短的是( )

 是一条河,
是一条河, 两地相距8千米,
两地相距8千米, 两地到
两地到 的距离分别为2千米,5千米,欲在
的距离分别为2千米,5千米,欲在 上的某点
上的某点 处修建一个水泵站,向
处修建一个水泵站,向 两地供水.现有如下四种铺设方案,则铺设的管道最短的是( )
两地供水.现有如下四种铺设方案,则铺设的管道最短的是( )
| A.过点P作PM⊥l交l于点M |
B.作点P关于l的对称点 ,连结 ,连结 Q,交l于点M Q,交l于点M |
| C.作线段PQ的垂直平分线交l于点M |
| D.过点Q作PM⊥l交l于点M |
A
此题应选A
解答:解:
A、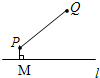
铺设的管道的长度为:PQ+PM=8+2=10(千米);
B、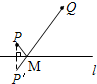
∵P′Q2=82-(5-2)2+(5+2)2=104,
∴铺设的管道的长度为:PM+QM=P′M+QM=P′Q=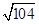 >10(千米);
>10(千米);
C、
铺设的管道的长度为: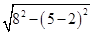 +5=
+5=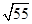 +3>7+3=10(千米);
+3>7+3=10(千米);
D、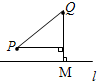
显然铺设的管道的长度PM+QM大于B中铺设的管道的长度,即PM+QM>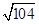 (千米).
(千米).
故选A.
解答:解:
A、

铺设的管道的长度为:PQ+PM=8+2=10(千米);
B、

∵P′Q2=82-(5-2)2+(5+2)2=104,
∴铺设的管道的长度为:PM+QM=P′M+QM=P′Q=
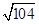 >10(千米);
>10(千米);C、

铺设的管道的长度为:
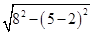 +5=
+5=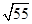 +3>7+3=10(千米);
+3>7+3=10(千米);D、

显然铺设的管道的长度PM+QM大于B中铺设的管道的长度,即PM+QM>
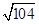 (千米).
(千米).故选A.

练习册系列答案
相关题目


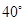 .若平行于OB的光线经点Q反射到P,则∠QPB=( )。
.若平行于OB的光线经点Q反射到P,则∠QPB=( )。 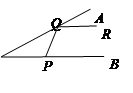
 ,∠1= 40°,则∠2 =( )。
,∠1= 40°,则∠2 =( )。
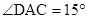 ,
,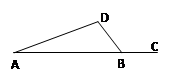
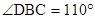 ,则
,则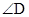 的度数是_____________
的度数是_____________ 则
则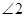 = .
= .