题目内容
已知a+x2=2003，b+x2=2004，c+x2=2005，且abc=6012，求
+
+
-
-
-
的值．
| a |
| bc |
| b |
| ca |
| c |
| ab |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
∵a+x2=2003，b+x2=2004，c+x2=2005，
∴b-a=1，c-b=1，c-a=2，
原式=
-（
+
+
）
=
-
=
=
，
∵b-a=1，c-b=1，c-a=2，abc=6012，
∴原式=
=
=
=
=
．
∴b-a=1，c-b=1，c-a=2，
原式=
| a2+b2+c2 |
| abc |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
=
| a2+b2+c2 |
| abc |
| bc+ac+ab |
| abc |
=
| a2+b2+c2-bc-ac-ab |
| abc |
=
| a(a-c)+b(b-a)+c(c-b) |
| abc |
∵b-a=1，c-b=1，c-a=2，abc=6012，
∴原式=
| -2a+b+c |
| 6012 |
=
| -2a+a+1+c |
| 6012 |
=
| 1+c-a |
| 6012 |
=
| 1+2 |
| 6012 |
=
| 1 |
| 2004 |
练习册系列答案
相关题目
的图象向左平移2个单位，再向下平移1个单位得到
的图象，则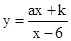
的图象经过B、E两点．则这个“反比例平移函数”的表达式为 ；这个“反比例平移函数”的图象经过适当的变换与某一个反比例函数的图象重合，请写出这个反比例函数的表达式．