题目内容
在x2+2y2=11,x2+2x+1,z(z2+1)=6,3x2+5x-3=0中,一元二次方程的个数是( )
分析:本题考查一元二次方程的定义,只含有一个未知数,未知项的次数为2的整式方程,叫一元二次方程.
一元二次方程必须满足三个条件:
(1)整式方程;
(2)未知数的最高次数是2;
(3)二次项系数不为0.
一元二次方程必须满足三个条件:
(1)整式方程;
(2)未知数的最高次数是2;
(3)二次项系数不为0.
解答:解:x2+2y2=11,含有两个未知数,故不符合题意;
z(z2+1)=6,未知数的次数为3,故不符合题意;
x2+2x+1,不是等式,故不符合题意;
3x2+5x-3=0,符合一元二次方程的定义;
故一元二次方程的个数是1个.
故选A.
z(z2+1)=6,未知数的次数为3,故不符合题意;
x2+2x+1,不是等式,故不符合题意;
3x2+5x-3=0,符合一元二次方程的定义;
故一元二次方程的个数是1个.
故选A.
点评:本题考查一元二次方程的定义,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
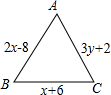 △ABC是等边三角形,表示其边长的代数式均已在图中标出,则
△ABC是等边三角形,表示其边长的代数式均已在图中标出,则