题目内容
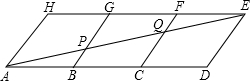
如图,用三个全等的菱形ABGH,BCFG,CDEF拼成平行四边形ADEH,连接AE与BG,CF分别交于P,Q。
(1)若AB=6,求线段BP的长;
(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论.
解:
(1)∵菱形ABGH,BCFG,CDEF是全等菱形,
∴BC=CD=DE=AB=6,
∴AD=3AB=3×6=18
∵BG∥DE;∴∠ABG=∠D,∠APB=∠AED.
∴△ABP∽△ADE
∴![]()
∴![]()
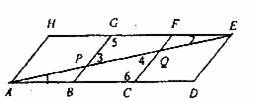
(2)图中的△EGP与△ACQ全等
证明:
∵菱形ABGH,BCFG,CDEF是全等的菱形; ∴AB=BC=EF=FG
∴AB+BC=EF+FC 即AC=EG
∵AD∥HE ∴∠1=∠2
∵BE∥CF ∴∠3=∠4
∴△EGP≌△ACQ

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目