题目内容
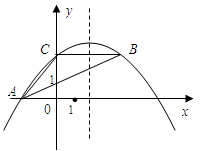
(本题12分)如图,抛物线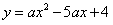 经过
经过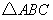 的三个顶点,已知
的三个顶点,已知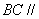
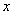 轴,点
轴,点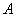 在
在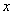 轴上,点
轴上,点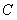 在
在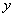 轴上,且
轴上,且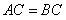 .
.
【小题1】(1)求抛物线的对称轴;
【小题2】(2)写出A,B,C三点的坐标(A,B,C三点的坐标只需写出答案),并求抛物线的解析式;
【小题3】(3)探究:若点
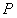 是抛物线对称轴上且在
是抛物线对称轴上且在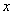 轴下方的动点,是否存在
轴下方的动点,是否存在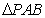 是等腰三角形.若存在,求出所有符合条件的点
是等腰三角形.若存在,求出所有符合条件的点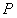 坐标;不存在,请说明理由.
坐标;不存在,请说明理由.
【小题1】(1)抛物线的对称轴
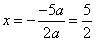 ………………………1分
………………………1分【小题2】(2)
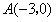
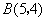
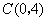 ………………………………3分
………………………………3分把点
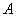 坐标代入
坐标代入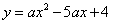 中,解得
中,解得
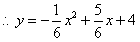 ……………………………2分
……………………………2分【小题3】(3)存在符合条件的点
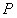 共有3个.以下分三类情形探索.
共有3个.以下分三类情形探索.设抛物线对称轴与
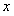 轴交于
轴交于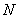 ,与
,与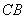 交于
交于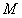 .
.过点
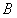 作
作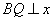 轴于
轴于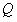 ,易得
,易得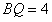 ,
,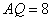 ,
,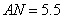 ,
,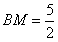
①以
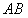 为腰且顶角为角
为腰且顶角为角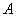 的
的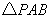 有1个:
有1个: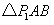 .
.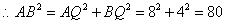
在
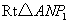 中,
中,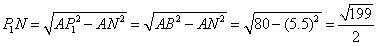
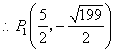 ……………………………2分
……………………………2分②以
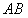 为腰且顶角为角
为腰且顶角为角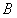 的
的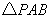 有1个:
有1个: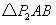 .
.在
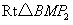 中,
中,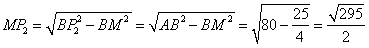
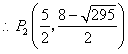 ……………………………2分
……………………………2分③以
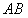 为底,顶角为角
为底,顶角为角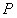 的
的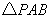 有1个,即
有1个,即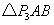 .
.画
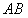 的垂直平分线交抛物线对称轴于
的垂直平分线交抛物线对称轴于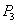 ,此时平分线必过等腰
,此时平分线必过等腰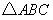 的顶点
的顶点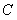 .
.过点
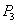 作
作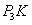 垂直
垂直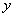 轴,垂足为
轴,垂足为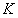 ,显然
,显然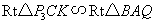 .
.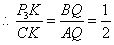 .
.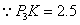
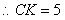 于是
于是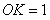
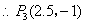 ………………………2分解析:
………………………2分解析:略

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目




 x2+3与x轴交于点A、B,与直线y=
x2+3与x轴交于点A、B,与直线y=