Question

某县为实现经济跨越，高度重视交通事业的发展．现有甲、乙两个工程队分别同时建筑两条水泥路面，所建路的长度y（m）与建筑的时间t（h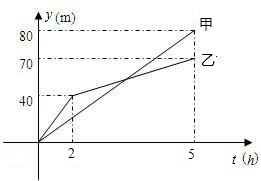）之间关系如下图所示，请根据图象提供的信息解答下列问题：
（1）乙队筑路到40m时，用了

 

h．筑路5h时，甲队比乙队多筑了

 

m．
（2）请你求出
①甲队在0≤x≤5的时段内，y与x的函数关系式．
②乙队在2≤x≤5的时段内，y与x的函数关系式．
（3）筑路多长时间时，甲、乙两队筑路的长度相等．

Answer 1

分析：（1）此题只要认真读图，可从中找到甲、乙两队各组数据；
（2）根据图中的信息利用待定系数法即可确定函数关系式；
（3）利用（2）中的函数关系式可以解决问题．

解答：解：（1）依题意得乙队开挖到40m时，用了2h，
开挖5h时甲队比乙队多挖了80-70=10m；

（2）设甲队在0≤x≤5的时段内y与x之间的函数关系式y=k₁x，
由图可知，函数图象过点（5，80），
∴5k₁=80，
解得k₁=16，
∴y=16x，
设乙队在2≤x≤5的时段内y与x之间的函数关系式为y=k₂x+b，
由图可知，函数图象过点（2，40）、（5，70），
∴

2k2+b=40 5k2+b=70

，
解得

k2=10 b=20

，
∴y=10x+20；

（3）由题意，得16x=10x+20，
解得x=

10

3

（h）．
∴当x为

10

3

h时，甲、乙两队所挖的河渠长度相等．

点评：此题主要考查学生对函数图象掌握情况及利用待定系数法求一次函数关系式，理解题意是解题的关键．