题目内容
用若干个小立方块搭一个几何体,使得它的左视图和俯视图如图所示,则所搭成的几何体中小立方块最多有( )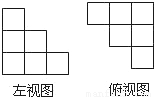
A.15个
B.14个
C.13个
D.12个
【答案】分析:根据三视图,该几何体底层最多有3+2+1个,第2层最多有2+2+1个,第3层最多有3个.分清物体的上下及左右的层数.
解答:解:综合左视图和俯视图,底层最多有3+2+1=6个,第二层最多有2+2+1=5个,第三层最多有1+1+1=3个,
因此所搭成的几何体中小立方体最多有6+5+3=14个,故选B.
点评:本题中正视图应该按小立方体最多的情况摆,然后根据从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,来分析小立方体的个数.
解答:解:综合左视图和俯视图,底层最多有3+2+1=6个,第二层最多有2+2+1=5个,第三层最多有1+1+1=3个,
因此所搭成的几何体中小立方体最多有6+5+3=14个,故选B.
点评:本题中正视图应该按小立方体最多的情况摆,然后根据从主视图上分清物体的上下和左右的层数,从俯视图上分清物体的左右和前后位置,来分析小立方体的个数.

练习册系列答案
相关题目




