题目内容
阅读材料:
我们将能完全覆盖平面图形的最小圆称为该平面图形的最小覆盖圆.
例如:线段AB的最小覆盖圆就是以线段AB为直径的圆.
操作探究:
(1)如图1:已知线段AB与其外一点C,作过A、B、C三点的最小覆盖圆;(不写作法,保留作图痕迹)
(2)边长为1cm的正方形的最小覆盖圆的半径是______cm;
如图2,边长为1cm的两个正方形并列在一起,则其最小覆盖圆的半径是______cm;
如图3,半径为1cm的两个圆外切,则其最小覆盖圆的半径是______cm.
联想拓展:
⊙O1的半径为8,⊙O2,⊙O3的半径均为5.
(1)当⊙O1、⊙O2、⊙O3两两外切时(如图4),则其最小覆盖圆的半径是______;
(2)当⊙O1、⊙O2、⊙O3两两相切时,(1)中的结论还成立吗?如果不成立,则其最小覆盖圆的半径是______,并作出示意图.
 操作探究:
操作探究:解:(1)作图为:
(2)①∵正方形的边长为1,由勾股定理,得
正方形的对角线长为:
 ,
,∴最小覆盖圆的半径是
 ;
;②)∵矩形的长为2,宽为1,由勾股定理,得
矩形的对角线长为:
 ,
,∴最小覆盖圆的半径是
 ;
;③∵两个半径为1的圆外切,
∴最小覆盖圆的半径是2.
 联想拓展:
联想拓展:解:(1)如图,O1O2=r1+r2=5+8=13=O1O3,
易知最小覆盖圆的圆心在O1O2中垂线上,设为O.
设O1O=x,则可以得到方程
R=8+x=5+

解之得x=

所以R=8+x=
 ;
;(2)由题意得示意图为:
∴最小覆盖圆的半径是大圆半径和小圆半径的和.
∴最小覆盖圆的半径是13.
故答案为:
 ,
, ,2,
,2, ,13.
,13.分析:(1)连接AC作AC的垂直平分线EF,作AB 的垂直平分线MN交EF于点P,连接AP,以点P为圆心,以AP为半径作圆.所以圆P是所求作的圆.
(2)边长为1的正方形的最小覆盖圆,就是以以正方形的对角线为直径的圆,从而求出答案;而两个正方形组合而成的矩形的最小覆盖圆就是以矩形的对角线为直径的圆;半径为1的两个外切圆的最小覆盖圆就是以两圆的半径和为半径的圆.
联想拓展
(1)易知最小覆盖圆的圆心在O1O2中垂线上,可得方程R=8+x=5+
 ,求解即可;
,求解即可;(2)当⊙O1与⊙O2内切,⊙O3与⊙O1、⊙O2外切时,(1)结论不成立,则最小覆盖圆的半径是大圆的半径加小圆的半径.从而求出结果.
点评:本题考查了两圆相切的性质,三角形的外接圆与圆心,正多边形和圆的关系及中垂线的性质,等腰三角形的性质,勾股定理的运用.

练习册系列答案
相关题目
 km.
km. m,即1m=
m,即1m=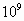 nm.我们通常使用的尺上的一小格是1mm,1mm=
nm.我们通常使用的尺上的一小格是1mm,1mm= m,可是,1mm=
m,可是,1mm= nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.
nm,易知1nm相当于1mm的一百万分之一.可想而知,1nm是多么的小.