ЬтФПФкШн
ЁОЬтФПЁПвбжЊЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуDЮЊжБЯпBCЩЯЕФвЛЖЏЕуЃЈЕуDВЛгыBЁЂCжиКЯЃЉЃЌвдADЮЊБпзїСтаЮADEFЃЈAЁЂDЁЂEЁЂFАДФцЪБеыХХСаЃЉЃЌЪЙЁЯDAF=60ЁуЃЌСЌНгCFЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуDдкБпBCЩЯЪБЃЌЧѓжЄЃКЂйBD=CFЃЛЂкAC=CF+CDЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDдкБпBCЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌНсТлAC=CF+CDЪЧЗёГЩСЂЃПШєВЛГЩСЂЃЌЧыаДГіACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЕуDдкБпCBЕФбгГЄЯпЩЯЧвЦфЫћЬѕМўВЛБфЪБЃЌВЙШЋЭМаЮЃЌВЂжБНгаДГіACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉAC=CF+CDВЛГЩСЂЃЌACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЪЧAC=CFЉCDЃЛЃЈ3ЃЉВЙЭММћНтЮіЃЌAC=CDЉCFЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнвбжЊЕУГіAF=ADЃЌAB=BC=ACЃЌЁЯBAC=ЁЯDAF=60ЁуЃЌЧѓГіЁЯBAD=CAFЃЌжЄЁїBADЁеЁїCAFЃЌЭЦГіCF=BDМДПЩЃЛ
ЃЈ2ЃЉЧѓГіЁЯBAD=ЁЯCAFЃЌИљОнSASжЄЁїBADЁеЁїCAFЃЌЭЦГіBD=CFМДПЩЃЛ
ЃЈ3ЃЉЛГіЭМаЮКѓЃЌИљОнSASжЄЁїBADЁеЁїCAFЃЌЭЦГіCF=BDМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉжЄУїЃКЁпСтаЮAFEDЃЌ
ЁрAF=ADЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=AC=BCЃЌЁЯBAC=60Ёу=ЁЯDAFЃЌ
ЁрЁЯBACЉЁЯDAC=ЁЯDAFЉЁЯDACЃЌ
МДЁЯBAD=ЁЯCAFЃЌ
ЁпдкЁїBADКЭЁїCAFжа
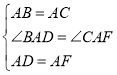
ЁрЁїBADЁеЁїCAFЃЌ
ЁрCF=BDЃЌ
ЁрCF+CD=BD+CD=BC=ACЃЌ
МДЂйBD=CFЃЌЂкAC=CF+CDЃЎ
ЃЈ2ЃЉНтЃКAC=CF+CDВЛГЩСЂЃЌACЁЂCFЁЂCDжЎМфДцдкЕФЪ§СПЙиЯЕЪЧAC=CFЉCDЃЌ
РэгЩЪЧЃКгЩЃЈ1ЃЉжЊЃКAB=AC=BCЃЌAD=AFЃЌЁЯBAC=ЁЯDAF=60ЁуЃЌ
ЁрЁЯBAC+ЁЯDAC=ЁЯDAF+ЁЯDACЃЌ
МДЁЯBAD=ЁЯCAFЃЌ
ЁпдкЁїBADКЭЁїCAFжа
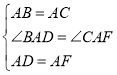 ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAFЃЌ
ЁрBD=CFЃЌ
ЁрCFЉCD=BDЉCD=BC=ACЃЌ
МДAC=CFЉCDЃЎ
ЃЈ3ЃЉAC=CDЉCFЃЎРэгЩЪЧЃК
ЁпЁЯBAC=ЁЯDAF=60ЁуЃЌ
ЁрЁЯDAB=ЁЯCAFЃЌ
ЁпдкЁїBADКЭЁїCAFжа
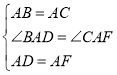 ЃЌ
ЃЌ
ЁрЁїBADЁеЁїCAFЃЌ
ЁрCF=BDЃЌ
ЁрCDЉCF=CDЉBD=BC=ACЃЌ
МДAC=CDЉCFЃЎ

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПЯжгаСНИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЌУПИізЊХЬЗжГЩШ§ИіЯрЭЌЕФЩШаЮЃЌЭПЩЋЧщПіШчЭМЫљЪОЃЌжИеыЕФЮЛжУЙЬЖЈЃЌЭЌЪБзЊЖЏСНИізЊХЬЃЌЛиД№вдЯТЮЪЬтЃК

дВ1 дВ2
дВ2 дВ1 | |||
(1)ВЙШЋБэИёЃКдВ1ЕФЫљгаПЩФмНсЙћга жжЃЌЗжБ№ЪЧ ЃЛ
дВ2ЕФЫљгаПЩФмНсЙћга жжЃЌЗжБ№ЪЧ .
(2)аДГіЃКзЊХЬЭЃжЙКѓжИеыжИЯђЭЌжжбеЩЋЧјгђЕФИХТЪКЭжСЩйгавЛжИеыжИЯђКьЩЋЧјгђЕФИХТЪ.
ЁОЬтФПЁПЙтУїЕчЦїГЌЪаЯњЪлУПЬЈНјМлЗжБ№ЮЊ190дЊЁЂ160дЊЕФAЁЂBСНжжаЭКХЕФЕчЗчЩШЃЌЯТБэЪЧНќСНжмЕФЯњЪлЧщПіЃК
ЯњЪлЪБЖЮ | ЯњЪлЪ§СП | ЯњЪлЪеШы | |
AжжаЭКХ | BжжаЭКХ | ||
ЕквЛжм | 2ЬЈ | 6ЬЈ | 1840дЊ |
ЕкЖўжм | 5ЬЈ | 7ЬЈ | 2840 дЊ |
ЃЈНјМлЁЂЪлМлОљБЃГжВЛБфЃЌРћШѓ=ЯњЪлЪеШы-НјЛѕГЩБОЃЉ
ЃЈ1ЃЉЧѓAЁЂBСНжжаЭКХЕФЕчЗчЩШЕФЯњЪлЕЅМлЃЛ
ЃЈ2ЃЉШєГЌЪазМБИдйВЩЙКетСНжжаЭКХЕФЕчЗчЩШЙВ40ЬЈЃЌет40ЬЈЕчЗчЩШШЋВПЪлГіКѓЃЌШєРћШѓВЛЕЭгк2660дЊЃЌЧѓAжжаЭКХЕФЕчЗчЩШжСЩйвЊВЩЙКЖрЩйЬЈЃП


