题目内容
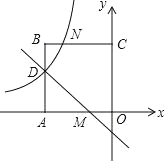
【题目】(2016山东省泰安市第25题)如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，3），点A在x轴的负半轴上，点D、M分别在边AB、OA上，且AD=2DB，AM=2MO，一次函数y=kx+b的图象过点D和M，反比例函数y=
的图象经过点D，与BC的交点为N．
（1）求反比例函数和一次函数的表达式；
（2）若点P在直线DM上，且使△OPM的面积与四边形OMNC的面积相等，求点P的坐标．
【答案】(1)、y=-x-1；(2)、（﹣10，9）或（8，﹣9）
【解析】
试题分析：(1)、由正方形OABC的顶点C坐标，确定出边长，及四个角为直角，根据AD=2DB，求出AD的长，确定出D坐标，代入反比例解析式求出m的值，再由AM=2MO，确定出MO的长，即M坐标，将M与D坐标代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；(2)、把y=3代入反比例解析式求出x的值，确定出N坐标，得到NC的长，设P（x，y），根据△OPM的面积与四边形OMNC的面积相等，求出y的值，进而得到x的值，确定出P坐标即可．
试题解析：(1)、∵正方形OABC的顶点C（0，3），∴OA=AB=BC=OC=3，∠OAB=∠B=∠BCO=90°，
∵AD=2DB， ∴AD=
AB=2， ∴D（﹣3，2）， 把D坐标代入y=
得：m=﹣6，
∴反比例解析式为y=﹣
， ∵AM=2MO，∴MO=
OA=1，即M（﹣1，0），
把M与D坐标代入y=kx+b中得：
，解得：k=b=﹣1，则直线DM解析式为y=﹣x﹣1；
(2)、把y=3代入y=﹣得：x=﹣2，∴N（﹣2，3），即NC=2，
设P（x，y）， ∵△OPM的面积与四边形OMNC的面积相等，
∴
（OM+NC）OC=OM|y|，即|y|=9， 解得：y=±9，
当y=9时，x=﹣10，当y=﹣9时，x=8，则P坐标为（﹣10，9）或（8，﹣9）．
