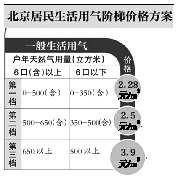
题目内容
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象经过点（0，3），且当x=1时，y有最小值2．
（1）求a，b，c的值；
（2）设二次函数y=k（2x+2）﹣（ax2+bx+c）
①若二次函数y=k（2x+2）﹣（ax2+bx+c）的图象与x轴的两个交点的横坐标x1，x2满足
，求k的值；
②请在二次函数y=ax2+bx+c与y=k（2x+2）﹣（ax2+bx+c）的图象上各找一个点M、N，且不论k为何值，这两个点始终关于x轴对称，求出点M、N的坐标（点M在点N的上方）．
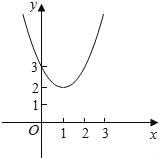
【答案】（1）a的值为1，b的值为﹣2，c的值为3；（2）①k=1或k=﹣5；②M（﹣1，6），N（﹣1，6）．
【解析】
试题分析：（1）用待定系数法求出抛物线解析式中的字母a，b，c，（2）①先化简抛物线y=k（2x+2）﹣（ax2+bx+c）的解析式，再用根与系数的关系表示出x1+x2=2（k+1），x1x2=3﹣2k，最后用
建立方程求解即可．②先设出点M的坐标，而点M，N关于x轴对称表示出点N的坐标，对称点的特点纵坐标互为相反数建立方程，得出（m+1）k=0，而不论k为何值，这两个点始终关于x轴对称，则有m+1=0，确定出m，最后得出点M，N的坐标．
试题解析：（1）由已知得：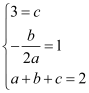
，
解得：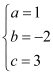
．
∴a的值为1，b的值为﹣2，c的值为3．
（2）①∵a=1，b=﹣2，c=3，
∴y=k（2x+2）﹣（ax2+bx+c）=﹣x2+2（k+1）x+2k﹣3，
∵二次函数y=k（2x+2）﹣（ax2+bx+c）的图象与x轴的两个交点的横坐标x1，x2，
∴x1+x2=2（k+1），x1x2=3﹣2k，
∴|x1﹣x2|=
，
解得：k=1或k=﹣5；
②∵a=1，b=﹣2，c=3，
∴y=x2﹣2x+3和y=﹣x2+2（k+1）x+2k﹣3，
设M（m，m2﹣2m+3），
∵点M，N始终关于x轴对称，
∴N（m，﹣m2+2（k+1）m+2k﹣3）
m2﹣2m+3=﹣（﹣m2+2（k+1）m+2k﹣3），
∴（m+1）k=0
∵不论k为何值，点M，N始终关于x轴对称，
∴m+1=0，
∴m=﹣1，
∴M（﹣1，6），N（﹣1，6）．
