题目内容
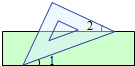 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的余角的度数是
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,则∠2的余角的度数是
- A.30°
- B.55°
- C.55°
- D.60°
D
分析:由两直线平行,内错角相等,即可求得∠3的度数,又由等腰直角三角形的性质,可求得∠2的度数,继而求得∠2的余角的度数.
解答: 解:∵a∥b,
解:∵a∥b,
∴∠3=∠1=15°,
∵∠ABC=45°,
∴∠2=∠ABC-∠3=45°-15°=30°,
∴∠2的余角的度数是:90°-∠2=60°.
故选D.
点评:此题考查了平行线的性质与余角的定义.此题比较简单,解题的关键是掌握两直线平行,内错角相等定理的应用,掌握数形结合思想的应用.
分析:由两直线平行,内错角相等,即可求得∠3的度数,又由等腰直角三角形的性质,可求得∠2的度数,继而求得∠2的余角的度数.
解答:
 解:∵a∥b,
解:∵a∥b,∴∠3=∠1=15°,
∵∠ABC=45°,
∴∠2=∠ABC-∠3=45°-15°=30°,
∴∠2的余角的度数是:90°-∠2=60°.
故选D.
点评:此题考查了平行线的性质与余角的定义.此题比较简单,解题的关键是掌握两直线平行,内错角相等定理的应用,掌握数形结合思想的应用.

练习册系列答案
相关题目
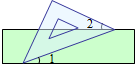 5、如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
5、如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )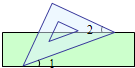
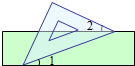 (2013•平凉)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
(2013•平凉)如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )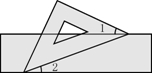 (2012•河池)如图,把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果∠1=25°,那么∠2的度数是( )
(2012•河池)如图,把一块含有45°角的直角三角板的两个顶点分别放在直尺的一组对边上.如果∠1=25°,那么∠2的度数是( )