题目内容
如图，AB∥CD，直线PQ分别交AB、CD于点E、F，FG是∠DEF的平分线，交AB于点G．若∠PFD=40°，那么∠FGB等于（ ）
A．80°
B．100°
C．110°
D．120°
【答案】分析：由于AB∥CD，可以得到∠EFG+∠FEG+∠DEG=180°，而∠PFA=∠EFG=40°，且EG是∠DEF的平分线，由此可以求出∠FEG；又∵∠EGB是△EFG的一个外角，由此求出∠EGB．
解答：解：∵AB∥CD，
∴∠EFG+∠FEG+∠DEG=180°，∠PFA=∠EFG=40°，
∵EG是∠DEF的平分线，
∴∠FEG=∠DEG=
（180°-∠EFG）=
（180°-40°）=70°，
∵∠FGB是△EFG的一个外角，
∴∠FGB=∠EFG+∠FEG=40°+70°=110°．
故选C．
点评：本题涉及到三角形内角和定理，角平分线的性质及三角形内角与外角的关系，属常规题目．
解答：解：∵AB∥CD，
∴∠EFG+∠FEG+∠DEG=180°，∠PFA=∠EFG=40°，
∵EG是∠DEF的平分线，
∴∠FEG=∠DEG=
（180°-∠EFG）=（180°-40°）=70°，∵∠FGB是△EFG的一个外角，
∴∠FGB=∠EFG+∠FEG=40°+70°=110°．
故选C．
点评：本题涉及到三角形内角和定理，角平分线的性质及三角形内角与外角的关系，属常规题目．
练习册系列答案
相关题目
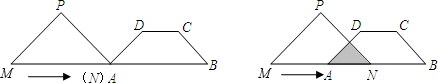
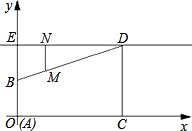横坐标为x，纵坐标为y．
如图，将网格中的三条线段AB、CD、EF沿网格线（水平和铅直方向）平移，使它们首尾相接构成三角形，至少需要移动
