题目内容
【题目】如图,点A,B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.求证:AC=CD.
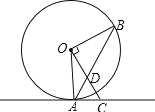
【答案】证明详见解析.
【解析】
试题分析:AC为圆的切线,利用切线的性质得到∠OAC为直角,再由OC与OB垂直,得到∠BOC为直角,由OA=OB,利用等边对等角得到一对角相等,再利用对顶角相等及等角的余角相等得到一对角相等,利用等角对等边即可得证.
试题解析:∵直线AC与⊙O相切,
∴OA⊥AC,
∴∠OAC=90°,即∠OAB+∠CAB=90°,
∵OC⊥OB,
∴∠BOC=90°,
∴∠B+∠ODB=90°,
而∠ODB=∠ADC,
∴∠ADC+∠B=90°,
∴OA=OB,
∴∠OAB=∠B,
∴∠ADC=∠CAB,
∴AC=CD.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目