题目内容
设n为不是1的自然数，若n是偶数，则n1=
；否则n1=3n+1．从n得到n1称之为“角谷变换”，若n1≠1，则又可对n1进行“角谷变换”，…，直到得到1为止，那么自然数100可经
| n | 2 |
25
25
次“角谷变换”得到1．分析：利用“角谷变换”的规律将100变换下去，直到1为之即可获得次数．
解答：解：∵若n是偶数，则n1=
；否则n1=3n+1，
∴100→50→25→76→38→19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1，
∴共经过25次“角谷变换”．
故答案为25．
| n |
| 2 |
∴100→50→25→76→38→19→58→29→88→44→22→11→34→17→52→26→13→40→20→10→5→16→8→4→2→1，
∴共经过25次“角谷变换”．
故答案为25．
点评：本题考查了数字规律类题目，解题的关键是仔细地观察题目提供的例子并从中找到正确的规律，并利用此规律解题．
练习册系列答案
名校课堂系列答案
相关题目
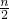；否则n1=3n+1．从n得到n1称之为“角谷变换”，若n1≠1，则又可对n1进行“角谷变换”，…，直到得到1为止，那么自然数100可经________次“角谷变换”得到1．