题目内容
如图，在一张长48分米，宽10分米的长方形纸片ABCD的边CD处放一平面镜，一束光线从纸片顶点A处射入，恰好由O点反射到B点，求光线在纸片上通过的距离．（提示：作点A关于的对称点A′，连结A′B，交CD于O点，则O点就是光的反射点）分析：根据轴对称的性质可得A′D=AD，A′O=AO，然后求出AA′，再利用勾股定理列式求出A′B，即为光线在纸片上通过的距离．
解答：解：∵点A关于平面镜的对称点为A′，
∴A′D=AD，A′O=AO，
∴AA′=2AD=2×10=20，
∵矩形ABCD的∠BAD=90°，
∴由勾股定理得，A′B=
=
=52分米，
∵AO+OB=A′O+OB=A′B，
∴光线在纸片上通过的距离为52分米．
∴A′D=AD，A′O=AO，
∴AA′=2AD=2×10=20，
∵矩形ABCD的∠BAD=90°，
∴由勾股定理得，A′B=
| AB2+AA′2 |
| 482+202 |
∵AO+OB=A′O+OB=A′B，
∴光线在纸片上通过的距离为52分米．
点评：本题考查了矩形的性质，轴对称的性质，利用轴对称的性质确定光线在纸片上通过的距离等于A′B是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在一张边长为40cm的正方形硬纸板的四角各剪掉一个同样大小的正方形，剩余部分折成一个无盖的长方体盒子（纸板的厚度忽略不计）．要使折成的长方体盒子的四个侧面的面积之和为800cm2，求剪掉的正方形的边长．
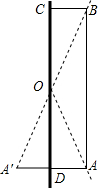如图，在一张长48分米，宽10分米的长方形纸片ABCD的边CD处放一平面镜，一束光线从纸片顶点A处射入，恰好由O点反射到B点，求光线在纸片上通过的距离．（提示：作点A关于的对称点A′，连结A′B，交CD于O点，则O点就是光的反射点）