题目内容
根据条件,求下列各题中m的取值或取值范围.
(1)函数y=(2m-1)x2有最小值;
(2)函数y=(m-2)x2,当x<0时,y随着x的增大而增大;
(3)y=(m+1)x2与y=2x2的函数图象形状相同;
(4)函数y=mxm2+m的图象是开口向下的抛物线.
(1)函数y=(2m-1)x2有最小值;
(2)函数y=(m-2)x2,当x<0时,y随着x的增大而增大;
(3)y=(m+1)x2与y=2x2的函数图象形状相同;
(4)函数y=mxm2+m的图象是开口向下的抛物线.
分析:(1)根据二次函数y=ax2+bx+c的性质:当a>0时,有最小值,可得2m-1>0,解不等式即可;
(2)根据二次函数y=ax2+bx+c的性质:当a<0时,在对称轴的左侧,y随x的增大而增大,得出m-2<0,解不等式即可;
(3)根据二次函数y=ax2+bx+c的性质:|a|相等时,函数图象形状相同,得出|m+1|=|2|,解方程即可;
(4)根据二次函数y=ax2+bx+c的性质:当a<0时,抛物线开口向下,得出m2+m=2,解方程,求出负数m即可.
(2)根据二次函数y=ax2+bx+c的性质:当a<0时,在对称轴的左侧,y随x的增大而增大,得出m-2<0,解不等式即可;
(3)根据二次函数y=ax2+bx+c的性质:|a|相等时,函数图象形状相同,得出|m+1|=|2|,解方程即可;
(4)根据二次函数y=ax2+bx+c的性质:当a<0时,抛物线开口向下,得出m2+m=2,解方程,求出负数m即可.
解答:解:(1)∵函数y=(2m-1)x2有最小值,
∴2m-1>0,
∴m>
;
(2)∵当x<0时,函数y=(m-2)x2的函数值y随着x的增大而增大,
∴m-2<0,
∴m<2;
(3)∵y=(m+1)x2与y=2x2的函数图象形状相同,
∴|m+1|=|2|,
∴m=1或-3;
(4)∵函数y=mxm2+m的图象是开口向下的抛物线,
∴m2+m=2且m<0,
∴m=-2或m=1,
∵m<0,
∴m=-2.
∴2m-1>0,
∴m>
| 1 |
| 2 |
(2)∵当x<0时,函数y=(m-2)x2的函数值y随着x的增大而增大,
∴m-2<0,
∴m<2;
(3)∵y=(m+1)x2与y=2x2的函数图象形状相同,
∴|m+1|=|2|,
∴m=1或-3;
(4)∵函数y=mxm2+m的图象是开口向下的抛物线,
∴m2+m=2且m<0,
∴m=-2或m=1,
∵m<0,
∴m=-2.
点评:本题考查了二次函数y=ax2+bx+c(a≠0)的性质,难度适中.用到的知识点:
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;此时函数有最小值.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;此时函数有最大值.
①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
| b |
| 2a |
| b |
| 2a |
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):
23、春林高级中学为了改善办学条件,2001年暑假对高中部内道长300米的操场投资修建塑胶跑道.请你根据图上所示数据完成下列各题(π取3.14):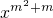 的图象是开口向下的抛物线.
的图象是开口向下的抛物线.