题目内容
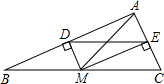 如图,点M在△ABC的BC边上(不与顶点B、C重合),分别作MD⊥AB、ME⊥AC,垂足D、E分别在两边AB、AC上,△ABM与△ACM的面积相等,且△BDM与△CEM的面积相等.若BD=2、CE=1,试求点A到BC边的距离.
如图,点M在△ABC的BC边上(不与顶点B、C重合),分别作MD⊥AB、ME⊥AC,垂足D、E分别在两边AB、AC上,△ABM与△ACM的面积相等,且△BDM与△CEM的面积相等.若BD=2、CE=1,试求点A到BC边的距离.
分析:分别设DM=x,ME=y,AD=z,AE=w,根据勾股定理求x、y的关系,并根据方程组求解x、y,同理即可求得z、w;根据△BDM与△CEM的面积相等的等量关系求解,根据面积法计算A到BC边的距离.
解答:解:由S△ABM=S△ACM知:BM=MC.记DM=x,ME=y,AD=z,AE=w.
由BM=MC及勾股定理得:22+x2=BM2=MC2=12+y2,
所以y2-x2=3.①
由S△BDM=S△CEM得:
•2•x=
•y•1,
所以y=2x②
把②代入①得:4x2-x2=3,x2=1,
故x=1,y=2,
又由勾股定理得:x2+z2=AM2=y2+w2,1+z2=22+w2,
即z2-w2=3③
由S△ABM=S△ACM得:
•x•(2+z)=
•y•(1+w),2+z=2+2w,
即z=2w④
把④代入③得:3w2=3,w2=1,故w=1,z=2,
从而S△ABC=
•1•4+
•2•2=4,BC=2BM=2•
=2
,
故点A到BC边的距离=
=
=
=
.
由BM=MC及勾股定理得:22+x2=BM2=MC2=12+y2,
所以y2-x2=3.①
由S△BDM=S△CEM得:
| 1 |
| 2 |
| 1 |
| 2 |
所以y=2x②
把②代入①得:4x2-x2=3,x2=1,
故x=1,y=2,
又由勾股定理得:x2+z2=AM2=y2+w2,1+z2=22+w2,
即z2-w2=3③
由S△ABM=S△ACM得:
| 1 |
| 2 |
| 1 |
| 2 |
即z=2w④
把④代入③得:3w2=3,w2=1,故w=1,z=2,
从而S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 22+12 |
| 5 |
故点A到BC边的距离=
| 2•S△ABC |
| BC |
| 2×4 | ||
2
|
| 4 | ||
|
| 4 |
| 5 |
| 5 |
点评:本题考查了勾股定理的正确运用,考查了在直角三角形中三角形面积计算,根据面积法求A到BC的距离是解本题的关键.

练习册系列答案
相关题目
 25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.
25、如图,点E在△ABC外部,点D在边BC上,DE交AC于F.若∠1=∠2=∠3,AC=AE,请说明△ABC≌△ADE的道理.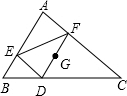 AC于点F.又知BC=5.
AC于点F.又知BC=5. 10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.
10、已知:如图,点D在△ABC的边BC上,DE∥AC交AB于E,DF∥AB交AC于F.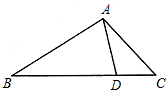 如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是
如图,点D在△ABC边BC上,且∠ADC=∠BAC,若AC=x,CD=x-2,BD=2x-2,则x的值是 如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.
如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB的中点,连接EF.