题目内容
 (2012•漳州二模)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,若把四边形ABCD绕着AD边的中点O顺时针旋转90°,试解决下列问题:
(2012•漳州二模)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,若把四边形ABCD绕着AD边的中点O顺时针旋转90°,试解决下列问题:(1)画出四边形ABCD旋转后的图形A′B′C′D′;
(2)求点C旋转过程中所经过的路径长;
(3)设点B旋转后的对应点为B′,求tan∠DAB′的值.
分析:(1)根据网格结构找出点A、B、C、D的对应点A′、B′、C′、D′的位置,然后顺次连接即可;
(2)根据勾股定理求出OC的长度,再利用弧长公式进行计算即可得解;
(3)利用网格结构,根据正切等于对边比邻边列式计算即可得解.
(2)根据勾股定理求出OC的长度,再利用弧长公式进行计算即可得解;
(3)利用网格结构,根据正切等于对边比邻边列式计算即可得解.
解答: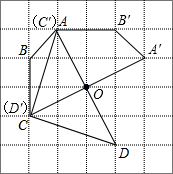 解:(1)如图所示,A′B′C′D′即为所求作的图形;
解:(1)如图所示,A′B′C′D′即为所求作的图形;
(2)根据勾股定理,OC=
=
,
点C旋转过程中所经过的路径长=
=
π;
(3)由图可知,tan∠DAB′=
=
=2.
 解:(1)如图所示,A′B′C′D′即为所求作的图形;
解:(1)如图所示,A′B′C′D′即为所求作的图形;(2)根据勾股定理,OC=
| 12+22 |
| 5 |
点C旋转过程中所经过的路径长=
90•π•
| ||
| 180 |
| ||
| 2 |
(3)由图可知,tan∠DAB′=
| B′D |
| AB′ |
| 4 |
| 2 |
点评:本题考查了利用旋转变换作图,弧长的计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
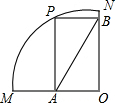 (2012•漳州二模)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在
(2012•漳州二模)如图,四边形PAOB是扇形OMN的内接矩形,顶点P在