题目内容
课外活动中一些学生分组参加活动,原来每组8人,后来重新编组,每组12人,这样比原来减少2组.这些学生共有
- A.48人
- B.56人
- C.60人
- D.72人
A
分析:设这些学生共有x人,先表示出原来和后来各多少组,其等量关系为后来的比原来的少2组,根据此列方程求解.
解答:设这些学生共有x人,
根据题意得: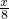 =
=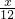 +2,
+2,
解这个方程得:x=48,
即这些学生共有48人.
故选A.
点评:此题考查的知识点是一元一次方程的应用,其关键是找出等量关系及表示原来和后来各多少组,难度一般.
分析:设这些学生共有x人,先表示出原来和后来各多少组,其等量关系为后来的比原来的少2组,根据此列方程求解.
解答:设这些学生共有x人,
根据题意得:
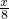 =
=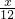 +2,
+2,解这个方程得:x=48,
即这些学生共有48人.
故选A.
点评:此题考查的知识点是一元一次方程的应用,其关键是找出等量关系及表示原来和后来各多少组,难度一般.

练习册系列答案
相关题目
某市准备购买一种新树苗进行绿化,甲、乙两个育苗基地对一次性购买树苗不低于1000株的用户均实行优惠.甲乙育苗基地优惠方式如下表
| 育苗基地 | 原售价 | 优惠政策 |
| 甲 | 4元/株 | 每株树苗按原售价的七五折出售 |
| 乙 | 4元/株 | 免收所购树苗中200株的费用,其余树苗按原售价的九折出售 |
①分别写出y1、y2与x之间的函数关系式(不要求写出自变量x的取值范围);
②若一次性购买1400株,在哪出购买所花的费用较少?为什么?
(2)若在甲、乙两处共购买2500株,并分别享受相应的优惠方式,则应在甲、乙两处分别购买多少株,才能使所花的费用最少?并求这个最少费用.
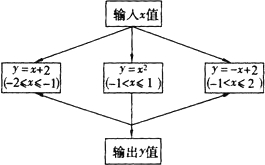 根据如图所示的程序计算函数值.若输入的x值为-1,则输出的结果为
根据如图所示的程序计算函数值.若输入的x值为-1,则输出的结果为


 如图所示,已知:点A(0,0),
如图所示,已知:点A(0,0),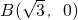 ,C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于
,C(0,1).在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第n个等边三角形的边长等于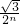

 如图.在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
如图.在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF. 如图,B、C、E、F在一条直线上,AC∥DE,且AC=DE,BE=CF,∠FED=50°,∠B=55°,则∠D=
如图,B、C、E、F在一条直线上,AC∥DE,且AC=DE,BE=CF,∠FED=50°,∠B=55°,则∠D=