Question

初二（3）班文艺委员小兰同学在布置“庆国庆、迎奥运”联欢会现场时，想从一块长为20cm，宽为8cm的长方形彩色纸板上剪下一个腰长为10cm的等腰三角形，并使其一个顶点在长方形的一边上，另两个顶点落在对边上，请你帮她设计出符合要求的等腰三角形，并求出等腰三角形的底边长．

Answer 1

分析：易得10为两直角边为6，8的直角三角形的斜边，那么可在长方形的长上截取OB为6，那么AB为10，符合题意的等腰三角形有一下三种情况：①AB=BE=10；②AB=BD=10；③AB=AC=10，利用等腰三角形三线合一的性质和勾股定理即可求得所得等腰三角形的底边长．

解答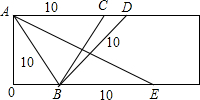：解：在长方形的长上截取OB为6，那么AB为10，符合题意的等腰三角形有一下三种情况：①AB=BE=10；②AB=BD=10；③AB=AC=10，
不同情况下的底边长为：
①利用勾股定理易得底边AE=

82+162；

=8

5

cm；
②利用等腰三角形三线合一定理及勾股定理易得底边AD=2

102-82

=12cm；
③底边BC=

82+(10-6)2

=4

5

cm；
∴底边长为12cm或4

5

cm或8

5

cm．

点评：解决本题的难点是利用所给图形得到长为10cm的线段长，关键是得到相关的等腰三角形．需要熟练掌握勾股定理和等腰三角形的性质．