Question

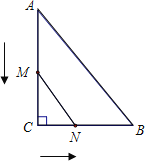
【题目】已知:如图，在Rt△ABC中，∠ACB=90，BC=6㎝，AB=10㎝．一动点M在边AC上从A向C以3㎝/s的速度匀速运动，另一动点N在边BC上同时从C向B以2㎝/s的速度匀速运动，当其中一个点到达终点时另一点也随之停止运动．设运动的时间为秒．

（1）当运动时间为多少秒时，△CMN的面积为5?

（2）当运动时间为多少秒时，以C、M、N为顶点的三角形与△ABC相似？

Answer 1

【答案】（1）1或；（2）或．

【解析】

（1）首先根据勾股定理求得AC的长，然后用x表示出线段MC和NC，利用三角形的面积计算公式列出方程求得时间即可；

（2）分△MCN∽△ACB时和△MCN∽△BCA时两种情况利用相似三角形的性质列出方程求得时间即可．

∵Rt△ABC中，∠ACB=90°，BC=6cm，AB=10cm，

∴AC==8，

∵动点M在边AC上从A向C以3cm/s的速度匀速运动，另一动点N在边BC上同时从C向B以2cm/s的速度匀速运动，运动时间为x秒，

∴AM=3xcm，CN=2xcm，

∴CM=（8-3x）cm，

（1）△CMN的面积为5cm2可得：×2x（8-3x）=5，

解得：x=1或x=，

答当运动时间x为1或秒时，△CMN的面积为5cm2；

（2）当△MCN∽△ACB时，，

即：，

解得：x=；

当△MCN∽△BCA时，，

即：，

解得：x=，

答：当运动时间x为或秒时，以C、M、N为顶点的三角形与△ABC相似．